题目内容
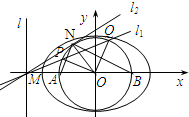
 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.(1)过M点的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
| 1 | 4 |
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;
(3)过M点作直线l2与圆相切于点N,设(2)中椭圆的两个焦点分别为F1,F2,求三角形△NF1F2面积.
分析:(1)由PQ为圆周的
,知∠POQ=
.所以O点到直线l1的距离为
,由此能求出l1的方程.
(2)设椭圆方程为
+
=1(a>b>0),半焦距为c,则
=2.由椭圆与圆O恰有两个不同的公共点,则a=1或b=1.由此能求出所求椭圆方程.
(3)设切点为N,则由题意得,在Rt△MON中,MO=2,ON=1,则∠NMO=30°,N点的坐标为(-
,
),由此能求出三角形△NF1F2面积.
| 1 |
| 4 |
| π |
| 2 |
| ||
| 2 |
(2)设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
(3)设切点为N,则由题意得,在Rt△MON中,MO=2,ON=1,则∠NMO=30°,N点的坐标为(-
| 1 |
| 2 |
| ||
| 2 |
解答:解:(1)∵PQ为圆周的
,∴∠POQ=
.∴O点到直线l1的距离为
.----(2分)
设l1的方程为y=k(x+2),∴
=
,∴k2=
.∴l1的方程为y=±
(x+2).---(5分)
(2)设椭圆方程为
+
=1(a>b>0),半焦距为c,则
=2.∵椭圆与圆O恰有两个不同的公共点,则a=1或b=1.-(6分)
当a=1时,c=
,b2=a2-c2=
,∴所求椭圆方程为x2+
=1;--(8分)
当b=1时,b2+c2=2c,∴c=1,∴a2=b2+c2=2.
所求椭圆方程为
+y2=1.---(10分)
(3)设切点为N,则由题意得,在Rt△MON中,MO=2,ON=1,则∠NMO=30°,
N点的坐标为(-
,
),---(11分)
若椭圆为
+y2=1.其焦点F1,F2
分别为点A,B故S△NF1F2=
×2×
=
,--(13分)
若椭圆为x2+
=1,其焦点为F1(-
,0),F2(
,0),
此时S△NF1F2=
×1×
=
--(15分)
| 1 |
| 4 |
| π |
| 2 |
| ||
| 2 |
设l1的方程为y=k(x+2),∴
| |2k| | ||
|
| ||
| 2 |
| 1 |
| 7 |
| ||
| 7 |
(2)设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
当a=1时,c=
| 1 |
| 2 |
| 3 |
| 4 |
| 4y2 |
| 3 |
当b=1时,b2+c2=2c,∴c=1,∴a2=b2+c2=2.
所求椭圆方程为
| x2 |
| 2 |
(3)设切点为N,则由题意得,在Rt△MON中,MO=2,ON=1,则∠NMO=30°,
N点的坐标为(-
| 1 |
| 2 |
| ||
| 2 |

若椭圆为
| x2 |
| 2 |
分别为点A,B故S△NF1F2=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
若椭圆为x2+
| 4y2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
此时S△NF1F2=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知直线l的方程为x=-2,且直线l与x轴交于点M,
已知直线l的方程为x=-2,且直线l与x轴交于点M,