Question

18．如图，给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$，它们的夹角为120°，点C在以O为圆心的$\widehat{AB}$上运动．若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$，其中x，y∈R，则x+2y的最大值是$\frac{2\sqrt{21}}{3}$．

Answer 1

分析 根据题意，建立直角坐标系，设出∠AOC=α，用cosα，sinα表示出$\overrightarrow{OC}$，由此求出x，y的值，再利用三角函数求x+2y的最大值．

解答 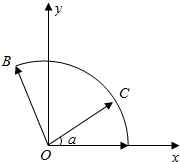解：根据题意，建立如图所示的坐标系，
则A（1，0），B（cos120°，sin120°），
即B（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）；
设∠AOC=α，则$\overrightarrow{OC}$=（cosα，sinα），
∵$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$，
∴（cosα，sinα）=（x，0）+（-$\frac{1}{2}$y，$\frac{\sqrt{3}}{2}$y）；
即cosα=x-$\frac{1}{2}$y，sinα=$\frac{\sqrt{3}}{2}$y，
解得：x=$\frac{\sqrt{3}}{3}$sinα+cosα，y=$\frac{2\sqrt{3}}{3}$sinα；
∴x+2y=$\frac{5\sqrt{3}}{3}$sinα+cosα=$\frac{2\sqrt{21}}{3}$sin（α+θ），其中tanθ=$\frac{\sqrt{3}}{5}$；
又sin（α+θ）≤1，
∴x+2y≤$\frac{2\sqrt{21}}{3}$．
故答案为：$\frac{2\sqrt{21}}{3}$．

点评 本题考查了平面向量知识的运用问题，也考查了三角函数的应用问题，解题的关键是确定x，y的关系式，是中档题目．