题目内容
已知椭圆C的离心率e= ,长轴的左右两个端点分别为A1(-2,0),A2(2,0);
,长轴的左右两个端点分别为A1(-2,0),A2(2,0);(1)求椭圆C的方程;
(2)点M在该椭圆上,且
 •
• =0,求点M到y轴的距离;
=0,求点M到y轴的距离;(3)过点(1,0)且斜率为1的直线与椭圆交于P,Q两点,求△OPQ的面积.
【答案】分析:(1)根据长轴端点判断椭圆位置和a,再由离心率和a2=b2+c2,求得b2,即可求出椭圆方程.
(2)先求出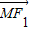 •
•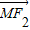 的解析式,把点M(x1,y2)代入椭圆,根据
的解析式,把点M(x1,y2)代入椭圆,根据 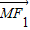 •
•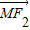 =0,即可求得结果.
=0,即可求得结果.
(3)椭圆与直线方程联立,得交点 坐标,进而结合三角形面积公式计算可得答案.
解答:解:(1)根据题意可知e=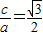 ,a=2
,a=2
∵a2=b2+c2=4
∴b2=1
所以椭圆的方程为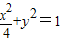
(2)设点M(x1,y1)在双曲线上
则y2=1-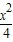
由椭圆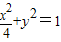
知F1(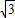 ,0),F2(-
,0),F2(-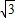 ,0)
,0)
∴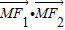 =x12-3+y12=0
=x12-3+y12=0
∴x12=
∴点M到y轴的距离为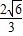 .
.
(3)由题意知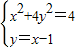
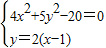 ,
,
解方程组得交点p(0,-1),P( ,
, ),
),
∴S△OPQ= (1×1+1×
(1×1+1× )=
)= .
.
点评:本题考查直线与椭圆的位置关系,解题时要注意对于圆锥曲线目前主要以定义及方程为主,对于直线与圆锥曲线的位置关系只要掌握直线与椭圆的相关知识即可.
(2)先求出
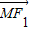 •
•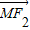 的解析式,把点M(x1,y2)代入椭圆,根据
的解析式,把点M(x1,y2)代入椭圆,根据 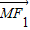 •
•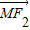 =0,即可求得结果.
=0,即可求得结果.(3)椭圆与直线方程联立,得交点 坐标,进而结合三角形面积公式计算可得答案.
解答:解:(1)根据题意可知e=
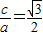 ,a=2
,a=2∵a2=b2+c2=4
∴b2=1
所以椭圆的方程为
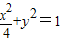
(2)设点M(x1,y1)在双曲线上
则y2=1-
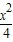
由椭圆
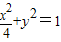
知F1(
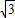 ,0),F2(-
,0),F2(-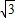 ,0)
,0)∴
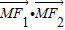 =x12-3+y12=0
=x12-3+y12=0∴x12=

∴点M到y轴的距离为
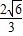 .
.(3)由题意知
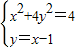
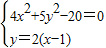 ,
,解方程组得交点p(0,-1),P(
 ,
, ),
),∴S△OPQ=
 (1×1+1×
(1×1+1× )=
)= .
.点评:本题考查直线与椭圆的位置关系,解题时要注意对于圆锥曲线目前主要以定义及方程为主,对于直线与圆锥曲线的位置关系只要掌握直线与椭圆的相关知识即可.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目