题目内容
已知椭圆C的离心率e=
| ||
| 2 |
分析:先将双曲线方程化简为标准形式,求出其焦点坐标,再由椭圆C的焦点与双曲线x2-2y2=4的焦点重合,可得到c的值,结合椭圆C的离心率e=
,可得到a的值,进而可得到答案.
| ||
| 2 |
解答:解:双曲线x2-2y2=4整理可得
-
=1
∴焦点坐标为(-
,0),(
,0)
∵椭圆C的焦点与双曲线x2-2y2=4的焦点重合
∴c=
∵椭圆C的离心率e=
,∴
=
∴a=2
∴b=
∴椭圆C的方程为:
+
=1
故答案为:
+
=1.
| x2 |
| 4 |
| y2 |
| 2 |
∴焦点坐标为(-
| 6 |
| 6 |
∵椭圆C的焦点与双曲线x2-2y2=4的焦点重合
∴c=
| 6 |
∵椭圆C的离心率e=
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
∴b=
| 2 |
∴椭圆C的方程为:
| x2 |
| 8 |
| y2 |
| 2 |
故答案为:
| x2 |
| 8 |
| y2 |
| 2 |
点评:本题主要考查椭圆的标准方程.考查基础知识的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,长轴的左右两个端点分别为A1(-2,0),A2(2,0);
,长轴的左右两个端点分别为A1(-2,0),A2(2,0);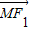 •
•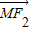 =0,求点M到y轴的距离;
=0,求点M到y轴的距离;