已知圆x2+y2+x-6y+m＝0和直线x+2y-3＝0交于P.Q两点.且OP⊥OQ.求该圆的圆心坐标和半径．题目和参考答案——青夏教育精英家教网——

题目内容

已知圆x²＋y²＋x－6y＋m＝0和直线x＋2y－3＝0交于P、Q两点，且OP⊥OQ(O为坐标原点)，求该圆的圆心坐标和半径．

答案：
解析：

将x＝3－2y代入圆方程得5y²－20y＋12＋m＝0，设P(x₁，y₁)、Q(x₂，y₂)，则y₁＋y₂＝4，且y₁y₂＝，∴x₁x₂＝(3－2y₁)(3－2y₂)，由OP⊥OQ，∴x₁x₂＋y₁y₂＝0，∴m＝3，此时Δ＞0，圆心坐标为(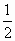－，3)，半径r＝．

练习册系列答案

小天才课时作业系列答案

一课四练系列答案

黄冈小状元满分冲刺微测验系列答案

新辅教导学系列答案

初中自主学习课时集训系列答案

阳光同学一线名师全优好卷系列答案

过关冲刺100分系列答案

圆梦图书课时达标100分系列答案

高效作业系列答案

倍速学习法系列答案

相关题目

已知圆x²＋y²＋x－6y＋m＝0与直线x＋2y－3＝0相交于两点P、Q，O为原点，若OP⊥OQ，求实数m的值．

已知圆x²＋y²＋x－6y＋m＝0与直线x＋2y－3＝0相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．

（12分）已知圆x²＋y²＋x－6y＋3=0与直线x＋2y－3=0的两个交点为P、Q，求以PQ为直径的圆的方程．

（12分）已知圆x²＋y²＋x－6y＋3=0与直线x＋2y－3=0的两个交点为P、Q，求以PQ

为直径的圆的方程．