题目内容
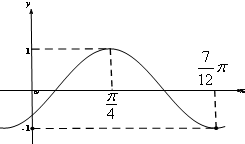
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的图象如图:将函数y=f(x)(x∈R)的图象向左平移
)的图象如图:将函数y=f(x)(x∈R)的图象向左平移 个单位,得函数y=g(x)的图象(g′(x)为g(x)的导函数),下面结论正确的是
个单位,得函数y=g(x)的图象(g′(x)为g(x)的导函数),下面结论正确的是
- A.函数g(x)是奇函数
- B.函数g′(x)在区间(-
 ,0)上是减函数
,0)上是减函数 - C.g(x)•g′(x)的最小值为-3
- D.函数g(x)的图象关于点(
 ,0)对称
,0)对称
D
分析:根据所给图象求出f(x)的解析式,通过平移求出g(x),进而求出g′(x),然后根据选项逐个检验即可.
解答:由图象知,A=1,函数f(x)的周期T=2(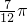 -
- )=
)= ,
,
由 =
= ,得ω=3,
,得ω=3,
由五点法作图知:3× +φ=
+φ= ,解得φ=-
,解得φ=- ,
,
所以f(x)=sin(3x- ),
),
g(x)=f(x+ )=sin[3(x+
)=sin[3(x+ )-
)- ]=sin(3x+
]=sin(3x+ )=cos3x,
)=cos3x,
g′(x)=-3sin3x,
因为g(-x)=cos(-3x)=cos3x=g(x),所以g(x)为偶函数,排除A;
g′(x)=-3sin3x在(- ,0)上不单调,故排除B;
,0)上不单调,故排除B;
g(x)•g′(x)=cos3x•(-3sin3x)=- sin6x,最小值为-
sin6x,最小值为- ,故排除C;
,故排除C;
由3x=kπ+ ,得x=
,得x=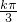 +
+ ,k∈Z,则g(x)=cos3x的对称中心为(
,k∈Z,则g(x)=cos3x的对称中心为(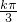 +
+ ,0)k∈Z,
,0)k∈Z,
当k=0时,对称中心为( ,0),
,0),
故选D.
点评:本题考查函数y=sin(ωx+φ)的图象变换,考查三角函数的单调性、奇偶性,考查学生综合运用所学知识解决问题的能力.
分析:根据所给图象求出f(x)的解析式,通过平移求出g(x),进而求出g′(x),然后根据选项逐个检验即可.
解答:由图象知,A=1,函数f(x)的周期T=2(
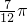 -
- )=
)= ,
,由
 =
= ,得ω=3,
,得ω=3,由五点法作图知:3×
 +φ=
+φ= ,解得φ=-
,解得φ=- ,
,所以f(x)=sin(3x-
 ),
),g(x)=f(x+
 )=sin[3(x+
)=sin[3(x+ )-
)- ]=sin(3x+
]=sin(3x+ )=cos3x,
)=cos3x,g′(x)=-3sin3x,
因为g(-x)=cos(-3x)=cos3x=g(x),所以g(x)为偶函数,排除A;
g′(x)=-3sin3x在(-
 ,0)上不单调,故排除B;
,0)上不单调,故排除B;g(x)•g′(x)=cos3x•(-3sin3x)=-
 sin6x,最小值为-
sin6x,最小值为- ,故排除C;
,故排除C;由3x=kπ+
 ,得x=
,得x=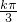 +
+ ,k∈Z,则g(x)=cos3x的对称中心为(
,k∈Z,则g(x)=cos3x的对称中心为(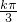 +
+ ,0)k∈Z,
,0)k∈Z,当k=0时,对称中心为(
 ,0),
,0),故选D.
点评:本题考查函数y=sin(ωx+φ)的图象变换,考查三角函数的单调性、奇偶性,考查学生综合运用所学知识解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目