题目内容
二次函数f（x）满足f（x+2）=f（-x+2），又f（0）=3，f（2）=1，若在[0，m]上有最大值3，最小值1，则m的取值范围是（ ）A．（0，+∞）
B．[2，+∞）
C．（0，2]
D．[2，4]
【答案】分析：由题意，二次函数f（x）满足f（2+x）=f（2-x），对称轴是x=2，可设二次函数为y=a（x-2）2+b，又f（0）=3，f（2）=1，由此得到关于两个参数a，b的方程组，解出a，b的值，求得二次函数的解析式；若f（x）在[0，m]上的最大值为3，最小值为1，求出1，3对应的自变量，再由二次函数的性质判断出参数的取值范围
解答：解：∵二次函数f（x）满足f（2+x）=f（2-x），
∴其对称轴是x=2，
可设其方程为y=a（x-2）2+b
∵f（0）=3，f（2）=1
∴
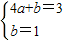
解得a=
，b=1
函数f（x）的解析式是y=
（x-2）2+1
∵f（0）=3，f（2）=1，f（x）在[0，m]上的最大值为3，最小值为1，
∴m≥2
又f（4）=3，由二次函数的性质知，m≤4
综上得2≤m≤4
故选D
点评：本题考查二次函数的在闭区间上的最值，解题的关键是用待定系数法求出函数的解析式，及熟练掌握二次函数的性质，判断出参数的取值范围，本题是二次函数考查的典型题．
解答：解：∵二次函数f（x）满足f（2+x）=f（2-x），
∴其对称轴是x=2，
可设其方程为y=a（x-2）2+b
∵f（0）=3，f（2）=1
∴
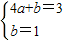
解得a=
，b=1函数f（x）的解析式是y=
（x-2）2+1∵f（0）=3，f（2）=1，f（x）在[0，m]上的最大值为3，最小值为1，
∴m≥2
又f（4）=3，由二次函数的性质知，m≤4
综上得2≤m≤4
故选D
点评：本题考查二次函数的在闭区间上的最值，解题的关键是用待定系数法求出函数的解析式，及熟练掌握二次函数的性质，判断出参数的取值范围，本题是二次函数考查的典型题．
练习册系列答案
相关题目