题目内容

5．在三角形ABC中，若sin（2A+B）=3sinB，求$\frac{tanA}{tanC}$的值．

分析 由题意可得sin[π+（A-C）]=3sin[π-（A+C）]，由三角函数公式整体法可得．

解答 解：∵在△ABC中sin（2A+B）=3sinB，
∴sin[π+（A-C）]=3sin[π-（A+C）]，
∴-sin（A-C）=3sin（A+C），
∴-sinAcosC+cosAsinC=3sinAcosC+3cosAsinC，
∴-2cosAsinC=4sinAcosC，
∴$\frac{tanA}{tanC}$=$\frac{\frac{sinA}{cosA}}{\frac{sinC}{cosC}}$=$\frac{sinAcosC}{cosAsinC}$=$\frac{-2}{4}$=-$\frac{1}{2}$

点评 本题考查三角函数恒等变换，涉及两角和与差的三角函数公式和整体思想以及同角三角函数基本关系，属中档题．

练习册系列答案
相关题目
15．M是抛物线y2=2x上-点，P点坐标为（3，$\frac{10}{3}$），设d是点M到准线的距离，要使d+|MP|最小，则点M的坐标为（2，2）．
16．设M={x|0≤x≤2}，N={y|0≤y≤2}，给出如图所示的四个图形：

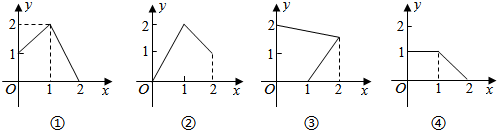
其中能表示从集合M到集合N的函数关系式的有（　　）
A．1个B．2个C．3个D．4个
13．等比数列的前n项和为Sn，且Sn=5n+5λ，则λ等于（　　）
A．-1B．-$\frac{1}{5}$C．$\frac{1}{5}$D．1
20．若f（x）是定义在R上的偶函数，且满足f（x）=-f（x+$\frac{3}{2}$），f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2008）的值为（　　）
A．-2B．0C．1D．2
10．设集合A=B={（x，y）|x，y∈R}，f是A到B的一个映射，且满足f：（x，y）→（xy，x-y），若集合B中的元素（a，b）在集合A中只有唯一的元素与之对应，则a，b应满足的关系式为（　　）
A．b2-2a=0B．b2+4a=0C．b2+2a=0D．b2-4a=0
17．设f（x）=$\frac{x-1}{x+1}$，f（$\frac{b}{a}$）+f（$\frac{a}{b}$）=0．
14．已知向量$\overrightarrow{a}$=（$\sqrt{3}$cosx，cosx），$\overrightarrow{b}$=（0，sinx），$\overrightarrow{c}$=（sinx，cosx），$\overrightarrow{d}$=（sinx，sinx）
（1）当x=-$\frac{π}{4}$时，求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ；
（2）当x∈[0，$\frac{π}{2}$]时，求$\overrightarrow{c}•\overrightarrow{d}$的最大值；
（3）设函数f（x）=（$\overrightarrow{a}$-$\overrightarrow{b}$）•（$\overrightarrow{c}$+$\overrightarrow{d}$），将函数f（x）的图象向右平移s个长度单位，向上平移t个长度单位（s，t＞0）后得到函数g（x）的图象，且g（x）=2sin2x+1，令$\overrightarrow{m}$=（s，t），求|$\overrightarrow{m}$|的最小值．
15．已知函数f（x）=（ax-b）ex（a≠0）．
①若f（x）≥-b恒成立，求f（1）的值；
②f（x）在（a，+∞）是单调减函数，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网