题目内容
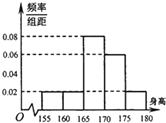 (2013•烟台一模)如图,某学校组织500名学生体检,按身高(单位:cm)分组:第1组[155,160),第2组[160,165),第3组[165,170),第4组[170,175),第5组[175,180],得到的频率分布直方图.
(2013•烟台一模)如图,某学校组织500名学生体检,按身高(单位:cm)分组:第1组[155,160),第2组[160,165),第3组[165,170),第4组[170,175),第5组[175,180],得到的频率分布直方图.(1)下表是身高的频数分布表,求正整数m,n的值;
(2)现在要从第1,2,3组中用分层抽样的方法抽取6人,第1,2,3组应抽取的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人,求至少有1人在第3组的概率.
| 区间 | 〔155,160〕 | 〔160,165〕 | 〔165,170〕 | 〔170,175〕 | 〔175,180〕 |
| 人数 | 50 | 50 | m | 150 | n |
分析:(1)根据频率分布直方图的高=
,频率=
,计算即可;
(2)根据分层抽样方法,按频数比例计算即可;
(3)根据古典概型的计算方法,先求所以可能的事件数,再求复合条件的可能事件数,然后求解即可.
| 频率 |
| 组距 |
| 频数 |
| 样本数 |
(2)根据分层抽样方法,按频数比例计算即可;
(3)根据古典概型的计算方法,先求所以可能的事件数,再求复合条件的可能事件数,然后求解即可.
解答:解:(1)由频率分布直方图,m=0.08×5×500=200,
n=0.02×5×500=50.
(2)∵第1、2、3组共有50+50+200=300人,
根据分层抽样的方法,第1组应抽6×
=1人;第2组应抽6×
=1人;第3组应抽6×
=4人.
(3)设第1组的同学为A;第2组的同学为B;第3组的同学为①、②、③、④,
则从六位同学中抽两位同学共有:(A,B),(A,①),(A,②),(A,③),(A,④),(B,①),(B,②),(B,③),(B,④),
(①,②),(①,③),(①,④),(②,③),(②,④),(③,④)15种可能,
其中2人都不在第3组的有:(A,B)共1种可能,
∴至少有一人在第3组的概率为1-
=
.
n=0.02×5×500=50.
(2)∵第1、2、3组共有50+50+200=300人,
根据分层抽样的方法,第1组应抽6×
| 50 |
| 300 |
| 50 |
| 300 |
| 200 |
| 300 |
(3)设第1组的同学为A;第2组的同学为B;第3组的同学为①、②、③、④,
则从六位同学中抽两位同学共有:(A,B),(A,①),(A,②),(A,③),(A,④),(B,①),(B,②),(B,③),(B,④),
(①,②),(①,③),(①,④),(②,③),(②,④),(③,④)15种可能,
其中2人都不在第3组的有:(A,B)共1种可能,
∴至少有一人在第3组的概率为1-
| 1 |
| 15 |
| 14 |
| 15 |
点评:本题考查频率分布直方图、分层抽样方法及古典概型的概率计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•烟台一模)从参加某次高三数学摸底考试的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
(2013•烟台一模)从参加某次高三数学摸底考试的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.