题目内容
【题目】公差不为零的等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 成等比数列,且该数列的前10项和为100,数列
成等比数列,且该数列的前10项和为100,数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() .
.
![]() Ⅰ
Ⅰ![]() 求数列
求数列![]() ,
,![]() 的通项公式;
的通项公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ,
,![]() ;(II)
;(II)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 通过等差数列
通过等差数列![]() 的公差
的公差![]() ,利用
,利用![]() 可知
可知![]() ,通过
,通过![]() 计算可知
计算可知![]() ;通过在
;通过在![]() 中令
中令![]() 可知首项
可知首项![]() ,当
,当![]() 时利用
时利用![]() 化简可知
化简可知![]() ,进而可知
,进而可知![]() ;
;![]() Ⅱ
Ⅱ![]() 通过
通过![]() 可知
可知![]() ,利用错位相减法可求数列
,利用错位相减法可求数列![]() 的前
的前![]() 项和,利用等比数列的求和公式可求数列
项和,利用等比数列的求和公式可求数列![]() 的前
的前![]() 项和,进而可知
项和,进而可知![]() ,通过函数
,通过函数![]() 的单调性计算即得结论.
的单调性计算即得结论.
![]() Ⅰ
Ⅰ![]() 依题意,等差数列
依题意,等差数列![]() 的公差
的公差![]() ,
,
![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
![]() ,即
,即![]() ,
,
整理得:![]() ,即
,即![]() ,
,
又![]() 等差数列
等差数列![]() 的前10项和为100,
的前10项和为100,
![]() ,即
,即![]() ,
,
整理得:![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
![]() 数列
数列![]() 是首项为1、公比为2的等比数列,
是首项为1、公比为2的等比数列,
![]() ;
;
![]() Ⅱ
Ⅱ![]() 由
由![]() 可知
可知![]() ,
,
记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,则
,则
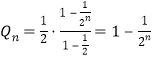 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
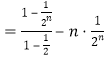
![]()
![]() ,
,
![]()
![]()
![]() ,
,
记![]() ,则
,则![]() ,
,
故数列![]() 随着n的增大而减小,
随着n的增大而减小,
又![]() ,
,![]() ,
,
![]() .
.

练习册系列答案
相关题目
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.