Question

【题目】已知圆C：x2＋y2＋2x－4y＋3＝0.

(1)若直线l过点(－2，0)且被圆C截得的弦长为2，求直线l的方程；

(2)从圆C外一点P向圆C引一条切线，切点为M，O为坐标原点，且|PM|＝|PO|，求|PM|的最小值．

Answer 1

【答案】（1）x＝－2或3x－4y＋6＝0（2）

【解析】

（1）根据直线l过点（-2，0）且被圆C截得的弦长为2，可得圆心C到l的距离，分类讨论，求出直线的斜率，即得直线的方程．
（2），求|PM|的最小值，即求出|PC|的最小值．

(1)x2＋y2＋2x－4y＋3＝0可化为(x＋1)2＋(y－2)2＝2，

当直线l的斜率不存在时，其方程为x＝－2，易求直线l与圆C的交点为A(－2，1)，B(－2，3)，|AB|＝2，符合题意；

当直线l的斜率存在时，设其方程为y＝k(x＋2)，即kx－y＋2k＝0，则圆心C到直线l的距离d＝＝1，

解得k＝，

所以直线l的方程为3x－4y＋6＝0.

综上，直线l的方程为x＝－2或3x－4y＋6＝0

(2)如图，PM为圆C的切线，连接MC，PC，则CM⊥PM，

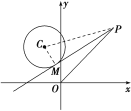
所以△PMC为直角三角形，

所以|PM|2＝|PC|2－|MC|2.

设P(x，y)，由(1)知C(－1，2)，|MC|＝，

因为|PM|＝|PO|，

所以(x＋1)2＋(y－2)2－2＝x2＋y2，

化简得点P的轨迹方程为2x－4y＋3＝0.

求|PM|的最小值，即求|PO|的最小值，也即求原点O到直线2x－4y＋3＝0的距离，代入点到直线的距离公式可求得|PM|的最小值为.