题目内容
| |||||||||||
答案：
解析：
解析：
(1) |
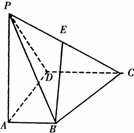
证：证明取PD的中点F，连结AF、EF E是PC的中点，∴EF∥CD且EF＝ 又AB∥CD，AB＝ BE∥AF又AF ∴BE∥平面PAD(6分) |
(2) |
解：∵PA、AB、AD两两垂直∴PA⊥平面ABCDAB⊥平面PAD(8分) ∴CD⊥平面PAD ∴CD⊥AF即CD⊥BE(10分) 且∠PDA为平面PCD与平面ABCD所成的角记α要使BE⊥平面PCD， 只须BE⊥PC，即AF⊥PD(12分) 在Rt△PAD中只须PA＝AD从而α＝ 因此，当平面PCD与平面ABCD成 |
CD(2分)
平面PAD，BE
平面PAD
(13分)
时，BE⊥平面BCD(14分)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，侧面PBC内有BE⊥PC于E，且BE＝
a，试在AB上找一点F，使EF∥平面PAD．
AB，点E，M分别为A1B，C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N
中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC＝
，
，
．
的大小．
中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC＝
，
，
．