题目内容
9.已知数列{an}中,a1=1,an+1=2an+2n;(1)求证:数列{$\frac{{a}_{n}}{{2}^{n}}$}成等差数列.
(2)根据(1)的结论,求an.
分析 (1)由an+1=2an+2n,两边同除以2n+1可得:$\frac{{a}_{n+1}}{{2}^{n+1}}-\frac{{a}_{n}}{{2}^{n}}=\frac{1}{2}$;
(2)根据等差数列的通项公式即可得出.
解答 (1)证明:∵an+1=2an+2n,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}-\frac{{a}_{n}}{{2}^{n}}=\frac{1}{2}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}成等差数列,首项为$\frac{1}{2}$,公差为$\frac{1}{2}$.
(2)解:根据(1)可得:${a}_{n}=\frac{1}{2}+\frac{1}{2}(n-1)$=$\frac{n}{2}$.
点评 本题考查了等差数列的通项公式,考查了变形能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.已知集合A={x|x2-4≤0},$B=\{x|\frac{x+1}{x-4}<0\}$,则A∪B=( )
| A. | {x|-1≤x<2} | B. | {x|-2≤x<4} | C. | {x|-1<x<4} | D. | {x|-4<x≤4} |
20.设复数z1和z2在复平面内的对应点关于左边原点对称,且z1=3-2i,则z1•z2=( )
| A. | -5+12i | B. | -5-12i | C. | -13+12i | D. | -13-12i |
17.设集合A={x|2x-1≥5},集合$B=\left\{{x|y=\frac{cosx}{{\sqrt{7-x}}}}\right\}$,则A∩B等于( )
| A. | (3,7) | B. | [3,7] | C. | (3,7] | D. | [3,7) |
4.已知命题p:已知实数a,b,则ab>0是a>0且b>0的必要不充分条件,命题q在曲线y=cosx上存在斜率为$\sqrt{2}$的切线,则下列判断正确的是( )
| A. | p是假命题 | B. | q是真命题 | C. | p∧(¬q)是真命题 | D. | (¬p)∧q是真命题 |
1.已知全集U=R,A={x|x<-1},B={x|x>1},则∁U(A∪B)=( )
| A. | {x|x>1} | B. | {x|x≤-1} | C. | {x|x>1或x<-1} | D. | {x|-1≤x≤1} |
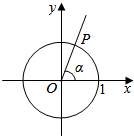 直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).
直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).