题目内容
已知函数![]() 的定义域为
的定义域为![]() ,值域为[-5,4];函数
,值域为[-5,4];函数 ![]() .
.
(Ⅰ) 求函数g(x)的最小正周期和最大值;
(Ⅱ) 当![]() , 且g(x) =5时, 求tan x.
, 且g(x) =5时, 求tan x.
(Ⅰ)当a>0时,T=2p, g(x)max=5;当a<0时,T=p, g(x)max=![]()
(Ⅱ) tan x=-![]()
解析:
f(x)=a(1-cos2x)-![]() sin2x+b
sin2x+b
=-a(cos2x+![]() sin2x)+a+b=-2a sin(2x+
sin2x)+a+b=-2a sin(2x+![]() )+a+b . ----------2分
)+a+b . ----------2分
∵x∈![]() ,∴2x+
,∴2x+![]() ,sin(2x+
,sin(2x+![]() )??
)??![]() . 显然a=0不合题意.---- -3分
. 显然a=0不合题意.---- -3分
(1) 当a>0时,值域为![]() ,即
,即![]() ----------5分
----------5分
(2) 当a<0时,值域为![]() ,即
,即![]() 6分
6分
(Ⅰ) 当a>0时,g(x)=3sinx-4cosx=5sin(x+j1), ∴T=2p, g(x)max=5;
当a<0时,g(x)= -3sinx+2cosx=![]() sin(x+j2),
sin(x+j2),
∴ T=p, g(x)max=![]() . 8分
. 8分
(Ⅱ)由上可知,
当a>0时, 由g(x)=5sin(x+j1),且tanj1=-![]() , g(x)max=5,此时x+j1=2kp +
, g(x)max=5,此时x+j1=2kp +![]() (k∈Z).
(k∈Z).
则x=2kp +![]() -j1(k∈Z), x∈(0, p),∴tanx=cot j1=-
-j1(k∈Z), x∈(0, p),∴tanx=cot j1=-![]() .10分
.10分
当a<0时, g(x)max=![]() <5,所以不存在符合题意的x. ---------12分
<5,所以不存在符合题意的x. ---------12分
综上,tan x=-![]() . -------------------13分
. -------------------13分

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为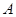 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.