题目内容
【题目】在平面直角坐标系中内动点P(x,y)到圆F:x2+(y﹣1)2=1的圆心F的距离比它到直线y=﹣2的距离小1.
(1)求动点P的轨迹方程;
(2)设点P的轨迹为曲线E,过点F的直线l的斜率为k,直线l交曲线E于A,B两点,交圆F于C,D两点(A,C两点相邻).
①若 ![]() =t
=t ![]() ,当t∈[1,2]时,求k的取值范围;
,当t∈[1,2]时,求k的取值范围;
②过A,B两点分别作曲线E的切线l1 , l2 , 两切线交于点N,求△ACN与△BDN面积之积的最小值.
【答案】
(1)解:由题意,动点P(x,y)到F(0,1)的距离比到直线y=﹣2的距离小1,
∴动点P(x,y)到F(0,1)的距离等于它到直线y=﹣1的距离,
∴动点P的轨迹是以F(0,1)为焦点的抛物线,其方程为x2=4y
(2)解:①由题意知,直线l方程为y=kx+1,代入抛物线得x2﹣4kx﹣4=0,
设(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=﹣4,
∵ ![]() =t
=t ![]() ,∴t=﹣
,∴t=﹣ ![]() ,
,
∴ ![]() =﹣t﹣
=﹣t﹣ ![]() +2=﹣4k2,
+2=﹣4k2,
∴t+ ![]() =4k2+2
=4k2+2
∵f(t)=t+ ![]() 在[1,2]上单调递增,∴2≤t+
在[1,2]上单调递增,∴2≤t+ ![]() ,
,
∴ ![]() ;
;
②y= ![]() ,y′=
,y′= ![]() ,
,
∴直线AN:y﹣ ![]() x12=
x12= ![]() x1(x﹣x1),BN:y﹣
x1(x﹣x1),BN:y﹣ ![]() x22=
x22= ![]() x1(x﹣x2),
x1(x﹣x2),
两式相减整理可得x= ![]() (x1+x2)=2k,
(x1+x2)=2k,
∴N(2k,﹣1),N到直线AB的距离d=2 ![]() ,
,
∵|AC|=|AF|﹣1=y1,|BD|=|BF|﹣1=y2,
∴|AC||BD|=1
∴△ACN与△BDN面积之积= ![]() =
= ![]() =1+k2,
=1+k2,
当且仅当k=0时,△ACN与△BDN面积之积的最小值为0
【解析】(1)由动点P(x,y)到F(0,1)的距离比到直线y=﹣2的距离小1,可得动点P(x,y)到F(0,1)的距离等于它到直线y=﹣1的距离,利用抛物线的定义,即可求动点P的轨迹W的方程;(2)①由题意知,直线l方程为y=kx+1,代入抛物线得x2﹣4kx﹣4=0,利用条件,结合韦达定理,可得t+ ![]() =4k2+2,利用函数的单调性,即可求k的取值范围;②求出直线AN,BN的方程,表示出面积,即可得出结论.
=4k2+2,利用函数的单调性,即可求k的取值范围;②求出直线AN,BN的方程,表示出面积,即可得出结论.

【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于 60分 | 60分 到79分 | 80分 到89分 | 不低 于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
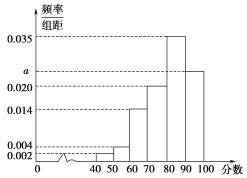
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)在等级为不满意市民中,老年人占![]() ,中青年占
,中青年占![]() ,现从该等级市民中按年龄分层抽取
,现从该等级市民中按年龄分层抽取![]() 人了解不满意的原因,并从中选取
人了解不满意的原因,并从中选取![]() 人担任整改督导员,求至少有一位老年督导员的概率;
人担任整改督导员,求至少有一位老年督导员的概率;
(3)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.![]()

