题目内容
已知函数f(x)=ax3+bx2+cx是R上的奇函数,且f(1)=2,f(2)=10
(1)确定函数![]() 的解析式;(2)用定义证明
的解析式;(2)用定义证明![]() 在R上是增函数;
在R上是增函数;
(3)若关于x的不等式f(x2-4)+f(kx+2k)<0在x∈(0,1)上恒成立,求k的取值范围。
(1)![]() (3)(-∞,1]
(3)(-∞,1]
解析:
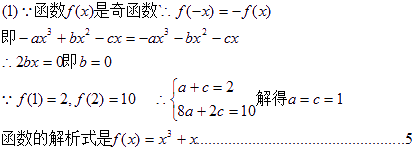
![]()
(2)证明:设x1,x2是R上的任意两个不相等的实数,且x1<x2, 则![]()
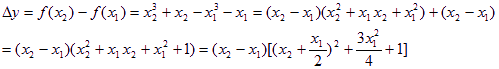
![]()
![]()
![]()
∴函数f(x)在R上是增函数。……………………………………………………………..10
(3)∵f(x2-4)+f(kx+2k)<0 ∴f(x2-4)<-f(kx+2k)=f(-kx-2k)
又因为f(x)是增函数,即x2-4<-kx-2k
∴x2+kx+2k-4<0在(0,1)上恒成立 ………………………………..12
法(一)令g(x) =x2+kx+2k-4 x∈(0,1)
![]() ∴k的取值范围是(-∞,1] ……………14
∴k的取值范围是(-∞,1] ……………14

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |