题目内容
17.过椭圆4x2+2y2=1的一个焦点F1的弦AB与另一个焦点F2所围成的△ABF2的周长是$2\sqrt{2}$.分析 由椭圆的方程知,长半轴a=4,利用椭圆的定义知,△ABF2的周长为4a,从而可得答案.
解答 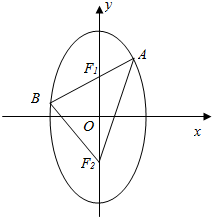 解:∵椭圆的方程为$\frac{{y}^{2}}{\frac{1}{2}}+\frac{{x}^{2}}{\frac{1}{4}}=1$,
解:∵椭圆的方程为$\frac{{y}^{2}}{\frac{1}{2}}+\frac{{x}^{2}}{\frac{1}{4}}=1$,
∴a=$\frac{\sqrt{2}}{2}$,b=$\frac{1}{2}$,又过焦点F1的直线与椭圆交于A,B两点,A,B与椭圆的另一个焦点F2构成△ABF2,
则△ABF2的周长l=|AB|+|AF2|+|BF2|=(|AF1|+|AF2|)+(|BF1|+|BF2|)=2a+2a=4a=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考椭圆的简单性质,着重考查椭圆定义的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.函数f(x)=x+lnx-2零点所在区间为( )
| A. | (0,1) | B. | (e,e2) | C. | (1,e) | D. | $(\frac{1}{2},1)$ |
8.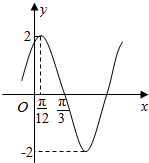 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
6.在复平面内,复数z=$\frac{1}{1+i}+{i^3}$所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.集合A={1,2}的非空真子集个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
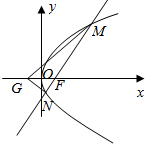 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2