题目内容
16.已知复数z1,z2满足|z1|≤1,-1≤Rez2≤1,-1≤Imz2≤1,若z=z1+z2,则z在复平面上对应的点组成的图形的面积为12+π.分析 由题意设出z1、z2,结合z=z1+z2得到z的轨迹(x-a)2+(y-b)2=1,由圆心变化得到z所对应点的图形,则面积可求.
解答 解:∵复数z1,z2满足|z1|≤1,-1≤Rez2≤1,-1≤Imz2≤1,
则可设z1=cosθ+isinθ,z2=a+bi(-1≤a≤1,-1≤b≤1),
由z=z1+z2,得z=(a+cosθ)+(b+sinθ)i,
设z=x+yi,则$\left\{\begin{array}{l}{x=a+cosθ}\\{y=b+sinθ}\end{array}\right.$,
∴(x-a)2+(y-b)2=1.
当a,b变化时,z点的轨迹如图: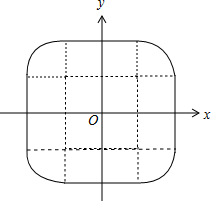
则z在复平面上对应的点组成的图形的面积为:
图中内部边长为2的正方形面积+四个长为2宽为1的长方形面积+四个四分之一圆的面积.
等于${2}^{2}+4×2×1+4×\frac{1}{4}π=12+π$.
故答案为:12+π.
点评 本题考查复数的代数表示法及其几何意义,考查数形结合的解题思想方法,关键是对题意的理解,属中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
11.设集合A={x|x2+x-6≤0},集合B为函数$y=\frac{1}{{\sqrt{x-1}}}$的定义域,则A∩B=( )
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
 如图,已知椭圆C中心在原点,焦点在x轴上,F1,F2分别为左右焦点,椭圆的短轴长为2,过F2的直线与椭圆C交于A,B两点,三角形F1BF2面积的最大值为$\sqrt{{a}^{2}-1}$(a>1).
如图,已知椭圆C中心在原点,焦点在x轴上,F1,F2分别为左右焦点,椭圆的短轴长为2,过F2的直线与椭圆C交于A,B两点,三角形F1BF2面积的最大值为$\sqrt{{a}^{2}-1}$(a>1).