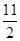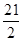题目内容
设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A.[1- ,1+ ,1+ ] ] |
B.(-∞,1- ]∪[1+ ]∪[1+ ,+∞) ,+∞) |
C.[2-2 ,2+2 ,2+2 ] ] |
D.(-∞,2-2 ]∪[2+2 ]∪[2+2 ,+∞) ,+∞) |
D
解析

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
直线 与圆
与圆 相交所得线段的长度为 ( )
相交所得线段的长度为 ( )
A. | B. | C. | D. |
已知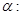 “
“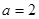 ”;
”;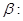 “直线
“直线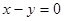 与圆
与圆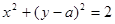 相切”.则
相切”.则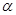 是
是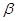 的( )
的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
直线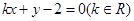 与圆
与圆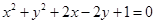 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相离 | D.与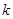 值有关 值有关 |
[2014·湖北模拟]若直线y=x+b与曲线y=3-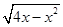 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )
A.[1-2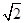 ,1+2 ,1+2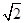 ] ] | B.[1-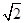 ,3] ,3] |
C.[-1,1+2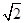 ] ] | D.[1-2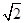 ,3] ,3] |
以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为( )
| A.x2+y2+2x=0 | B.x2+y2+x=0 |
| C.x2+y2﹣x=0 | D.x2+y2﹣2x=0 |
若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
| A.2 | B.3 | C.4 | D.6 |
 ,0)引直线l与曲线
,0)引直线l与曲线 相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( )
相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( ) B.
B. C.
C. D.
D.