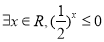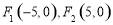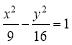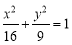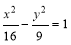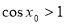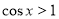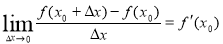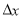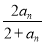题目内容
已知离心率 的椭圆
的椭圆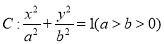 一个焦点为
一个焦点为 .
.
(1)求椭圆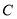 的方程;
的方程;
(2) 若斜率为1的直线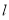 交椭圆
交椭圆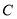 于
于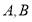 两点,且
两点,且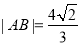 ,求直线
,求直线 方程.
方程.
(1) 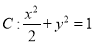 ;
;
【解析】(2) 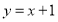 或
或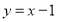 .
.
试题分析:(1)由焦点坐标、离心率及 解方程即可;
解方程即可;
(2)可以联立直线L与椭圆方程消去y,得到关于x的一元二次方程,然后利用弦长公式建立方程求出斜率截距m即可.
试题解析:【解析】
(1)由题知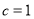 ,
,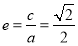 ,∴
,∴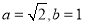 ,3分
,3分
∴椭圆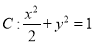 .4分
.4分
(2) 设直线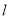 方程为
方程为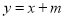 ,点
,点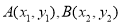 ,
,
由方程组 6分
6分
化简得: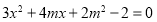 ,
,
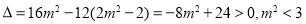 .8分
.8分
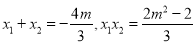
∴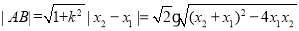 ,9分
,9分
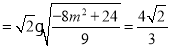 ,
,
解得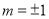 .11分
.11分
∴直线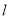 方程
方程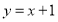 或
或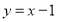 .12分
.12分
考点:1.椭圆的标准方程;2.直线与圆锥曲线相交;3. 弦长公式.

练习册系列答案
相关题目