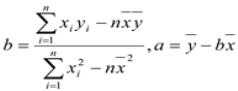题目内容
【题目】设L为曲线C：y＝
在点(1,0)处的切线．
(1)求L的方程；
(2)证明：除切点(1,0)之外，曲线C在直线L的下方．
【答案】（1）y＝x－1
（2）见解析
【解析】(1)设f(x)＝
，则f′(x)＝
所以f′(1)＝1，所以L的方程为y＝x－1.
(2)证明：令g(x)＝x－1－f(x)，则除切点之外，曲线C在直线L的下方等价于g(x)>0(x>0，x≠1)．
g(x)满足g(1)＝0，且
g′(x)＝1－f′(x)＝
.
当0＜x＜1时，x2－1＜0，ln x＜0，所以g′(x)＜0，故g(x)单调递减；
当x>1时，x2－1>0，ln x>0，所以g′(x)>0，故g(x)单调递增．
所以，g(x)>g(1)＝0(x>0，x≠1)．
所以除切点之外，曲线C在直线L的下方．
练习册系列答案
相关题目
