题目内容
(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1

(I)若M、N分别是AB,A1C的中点,求证:MN//平面BCC1B1
(II)若三棱柱ABC-A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC。
【答案】
(Ⅰ)证明:连接 推出MN
推出MN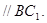 MN//
MN// .
.
(Ⅱ)将平面 展开到与平面
展开到与平面 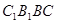 共面,
共面,
 到
到 的位置,此时
的位置,此时 为菱形,
为菱形,
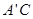 即为
即为 的最小值,
的最小值,
由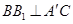 ,推出
,推出 ,
, ,即
,即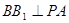 ,
, ,
,
进一步得到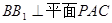 .
.
【解析】
试题分析:(Ⅰ)证明:连接 则
则 ,因为AM=MB,所以MN
,因为AM=MB,所以MN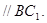 ……………3分
……………3分
又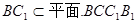 ,
,

所以MN// .…………5分
.…………5分
(Ⅱ)将平面 展开到与平面
展开到与平面 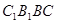 共面,
共面,
 到
到 的位置,此时
的位置,此时 为菱形,…………7分
为菱形,…………7分
可知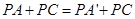
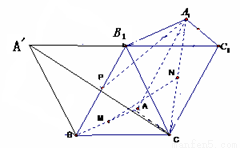
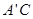 即为
即为 的最小值,…………9分
的最小值,…………9分
此时,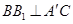 ,
,
所以 ,
, ,即
,即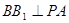 ,
, ,
,
所以,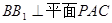 .……………12分
.……………12分
考点:本题主要考查立体几何中的平行关系、垂直关系。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,(2)小题,将立体问题转化成平面问题,这也是解决立体几何问题的一个基本思路。。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目