Question

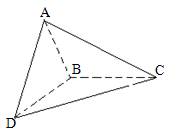
（08年唐山市一中调研一理） 设△ABC和△DBC所在的两个平面互相垂直，且AB=BC=BD，∠ABC=∠DBC=120°

   （I）求证；   

   （II）求二面角A―BD―C的大小.

 

 

Answer 1

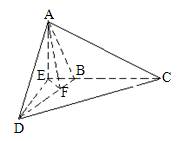
解析：（I）过A作AE垂直CB延长线于E，由已知则AE⊥平面DBC，连接DE则DE是AD在平面DBC内的射影，由三垂线定理，则CB⊥AD

   （II）作EF垂直DB于F，连接AF，则由三垂线定理，∠AFE为二面角A―DB―C的平面角的补角，设BC=a，则DE=AE=，BE=，所以EF=，tan∠AFE=2， 

因而所求二面角A―DB―C的大小为