题目内容
直角三角形斜边长为8,求面积和周长的最大值.
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:设直角三角形的直角边分别为x,y;则x2+y2=64;利用基本不等式求最值.
解答:
解:设直角三角形的直角边分别为x,y;
则x2+y2=64;
故周长x+y+8≤8+2
=8+8
,
(当且仅当x=y=4
时,等号成立),
故周长的最大值为8+8
;
面积S=
xy≤
•
=16,
(当且仅当x=y=4
时,等号成立),
故面积的最大值为16.
则x2+y2=64;
故周长x+y+8≤8+2
|
| 2 |
(当且仅当x=y=4
| 2 |
故周长的最大值为8+8
| 2 |
面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| x2+y2 |
| 2 |
(当且仅当x=y=4
| 2 |
故面积的最大值为16.
点评:本题考查了基本不等式在求最值中的应用,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
如图,汉若塔问题是指有3根杆子A、B、C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的上面.把B杆上的5个碟子全部移到A杆上,最少需要移动( )


| A、31次 | B、32次 |
| C、33次 | D、35次 |
在四边形ABCD中,若
=
+
,则四边形ABCD的形状一定是( )
| AC |
| AB |
| AD |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
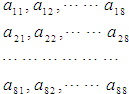 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=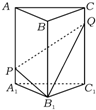 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为