Question

【题目】如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为(　　)

(A) (B)- (C) (D)-

Answer 1

【答案】A

【解析】如图,

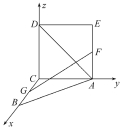
正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点.

以C为原点建立空间直角坐标系Cxyz,

A(0,2,0),B(2,0,0),D(0,0,2),G(1,0,0),F(0,2,1),

=(0,-2,2),=(-1,2,1),

∴||=2,||=,·=-2,

∴cos<,>==-.

∴直线AD与GF所成角的余弦值为.

【误区警示】本题容易忽视异面直线所成角的范围而误选B.