题目内容
(2013•丽水一模)若函数f(x)=x3+ax2+bx+c在R上有三个零点,且同时满足:
①f(1)=0;
②f(x)在x=0处取得极大值;
③f(x)在区间(0,1)上是减函数.
(Ⅰ)当a=-2时,求y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若g(x)=1-x,且关于x的不等式f(x)≥g(x)的解集为[1,+∞),求实数a的取值范围.
①f(1)=0;
②f(x)在x=0处取得极大值;
③f(x)在区间(0,1)上是减函数.
(Ⅰ)当a=-2时,求y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若g(x)=1-x,且关于x的不等式f(x)≥g(x)的解集为[1,+∞),求实数a的取值范围.
分析:(Ⅰ)首先由题目给出的条件求出b的值,a的范围及a和c的关系,然后把a=-2代入函数f(x)的解析式,求出函数在x=2时的导数,利用点斜式求y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)把c用a表示,化简不等式f(x)≥g(x),把该不等式恒成立转化为二次不等式恒成立的问题,然后利用“三个二次”的结合列式求解实数a的取值范围.
(Ⅱ)把c用a表示,化简不等式f(x)≥g(x),把该不等式恒成立转化为二次不等式恒成立的问题,然后利用“三个二次”的结合列式求解实数a的取值范围.
解答:解:由f(1)=0得:1+a+b+c=0,f'(x)=3x2+2ax+b.
因为f(x)在x=0处取得极大值,所以 f'(0)=0,即b=0.
因为f(x)在区间(0,1)上是减函数,则f'(1)≤0,所以 3+2a≤0,所以 a≤-
.
(Ⅰ) 当a=-2时,f'(x)=3x2-4x,所以 f'(2)=4
由a=-2,b=0,1+a+b+c=0,所以 c=1
所以 f(x)=x3-2x2+1,则点(2,f(2))为(2,1),
所以切线方程为:y-1=4(x-2),即y=4x-7.
(Ⅱ) f(x)-g(x)=x3+ax2-1-a-1+x=x3+ax2+x-a-2,f(1)-g(1)=1+a+1-a-2=0
要使f(x)≥g(x)的解集为[1,+∞),必须x2+(1+a)x+(a+2)≥0恒成立
所以,△=(1+a)2-4(a+2)<0(1),或
(2)
解得:(1)得1-2
<a<1+2
,解(2)得-2≤a≤1-2
.
又∵a≤-
,∴-2≤a≤-
.
所以使不等式f(x)≥g(x)的解集为[1,+∞)的实数a的取值范围是[-2,-
].
因为f(x)在x=0处取得极大值,所以 f'(0)=0,即b=0.
因为f(x)在区间(0,1)上是减函数,则f'(1)≤0,所以 3+2a≤0,所以 a≤-
| 3 |
| 2 |
(Ⅰ) 当a=-2时,f'(x)=3x2-4x,所以 f'(2)=4
由a=-2,b=0,1+a+b+c=0,所以 c=1
所以 f(x)=x3-2x2+1,则点(2,f(2))为(2,1),
所以切线方程为:y-1=4(x-2),即y=4x-7.
(Ⅱ) f(x)-g(x)=x3+ax2-1-a-1+x=x3+ax2+x-a-2,f(1)-g(1)=1+a+1-a-2=0
|
要使f(x)≥g(x)的解集为[1,+∞),必须x2+(1+a)x+(a+2)≥0恒成立
所以,△=(1+a)2-4(a+2)<0(1),或
|
解得:(1)得1-2
| 2 |
| 2 |
| 2 |
又∵a≤-
| 3 |
| 2 |
| 3 |
| 2 |
所以使不等式f(x)≥g(x)的解集为[1,+∞)的实数a的取值范围是[-2,-
| 3 |
| 2 |
点评:本题考查学生会利用导数求曲线上过某点切线的方程,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件,考查了数学转化思想方法解答(Ⅱ)的关键是把三次不等式恒成立转化为常见的二次不等式恒成立问题,是难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
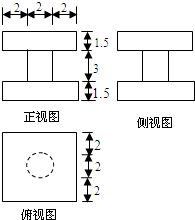 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),