题目内容
要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：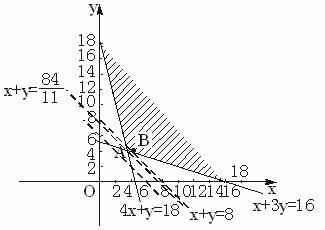
今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数最少.
解:设需截甲种钢管x根，乙种钢管y根，则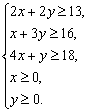
作出可行域(如下图)；
目标函数为z=x＋y.
作出一组平行直线x＋y=t中(t为参数)经过可行域内的点且和原点距离最近的直线，此直线经过直线4x＋y=18和直线x＋3y=16的交点A(
，
)，直线方程为x＋y=
.由于
和
都不是整数，所以可行域内的点(
，
)不是最优解.
经过可行域内的整点且与原点距离最近的直线是x＋y=8，经过的整点是B(4，4)，它是最优解.
答:要截得所需三种规格的钢管，且使所截两种钢管的根数最少，方法是截甲种钢管、乙种钢管各4根.
点评:此例的解法是，先依条件列出不等式组，作出可行域，不考虑x、y为非负整数的条件，求出符合题中其他条件的最优解，然后看此最优解是否为非负整数解，若是非负整数解，则即为所求.若不是非负整数解，则应求出经过可行域内的非负整数解且与原点距离最远(或最近)的点的直线，点(4,4)也是可行域内与过点(
, 
)、斜率为－1的直线距离最近的点，这个非负整数解就是最优解.
．要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：
| 规格类型
| A规格 | B规格 | C规格 | ||
| 甲种钢管 | 2 | 1 | 4 | ||
| 乙种钢管 | 2 | 3 | 1 |
今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数
规格类型 钢管类型 | A规格 | B规格 | C规格 |
甲种钢管 | 2 | 1 | 4 |
乙种钢管 | 2 | 3 | 1 |
今需A、B、C三种规格的钢管各13、16、18根,问各截这两种钢管多少根可得所需三种规格钢管,且使用钢管根数最少?
要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：
|
钢管类型 | A规格 | B规格 | C规格 |
| 甲种钢管 | 2 | 1 | 4 |
| 乙种钢管 | 2 | 3 | 1 |
规格类型今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根，可得所需三种规格钢管，且使所用钢管根数最少？