题目内容
(本小题满分12分)
已知平面区域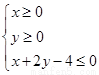
被圆C及其内部所覆盖．
(1)当圆C的面积最小时，求圆C的方程；
(2)若斜率为1的直线l与(1)中的圆C交于不同的两点A、B，且满足CA⊥CB，求直线l的方程．
【答案】
(1) (x－2)2＋(y－1)2＝5. (2) y＝x－1±
【解析】
试题分析：(1)由题意知此平面区域表示的是以O(0,0)，P(4,0)，Q(0,2)构成的三角形及其内部，且△OPQ是直角三角形，
∵覆盖它的且面积最小的圆是其外接圆．∴圆心是(2,1)，半径是，
∴圆C的方程是(x－2)2＋(y－1)2＝5.
(2)设直线l的方程是：y＝x＋b.∵CA⊥CB，∴圆心C到直线l的距离是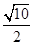
，
即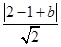
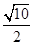＝.解之得，b＝－1±.
∴直线l的方程是：y＝x－1±.
考点：圆的方程及直线与圆相交问题
点评：(1)中首要分析出面积最小的圆是三角形的外接圆，(2)中直线与圆相交时圆心到直线的距离，弦长的一半及圆的半径构成直角三角形，常利用勾股定理寻找关系式
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
