题目内容
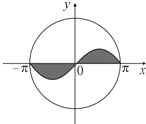如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是分析：先求构成试验的全部区域为圆内的区域的面积，再利用积分知识可得正弦曲线y=sinx与x轴围成的区域记为M的面积为S=2∫0πsinxdx=-2cosx0π=4，代入几何概率的计算公式可求
解答：解：构成试验的全部区域为圆内的区域，面积为π3
正弦曲线y=sinx与x轴围成的区域记为M，面积为S=2∫0πsinxdx=-2cosx|0π=4
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
故答案为：
正弦曲线y=sinx与x轴围成的区域记为M，面积为S=2∫0πsinxdx=-2cosx|0π=4
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
| 4 |
| π3 |
故答案为：
| 4 |
| π3 |
点评：本题主要考查了利用积分求解曲面的面积，几何概率的计算公式的运用，属于中档试题，具有一定的综合性，但难度不大．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
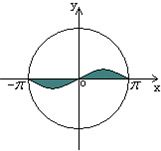如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2012•吉林二模）如图，圆O：x2+y2=
如图，圆O：x2+y2=
如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是（ ）
