题目内容
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是A1B1和BB1的中点,那么直线AM与CN所成的角的余弦值是( ) [来源:学,科,网]
A.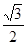 | B.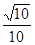 | C.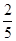 | D.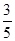 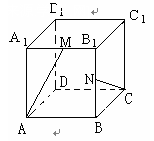 |
C
解析∵M、N分别是A1B1、BB1的中点,而A1B1=BB1=1,∴B1M=B1N=1/2。
∵B1E是MA平移所得,∴B1E∥MA、B1E=MA,∴AEB1M是平行四边形,∴AE=B1M=1/2,
∴BE=AB-AE=1-1/2=1/2。
∵B1F是NC平移所得,∴B1F∥NC、B1F=NC,∴CFB1N是平行四边形,∴FC=B1N=1/2。
∵ABCD-AB1C1D1是正方体,∴ABCD是正方形,∴BE⊥BC,
∴CE^2=BE^2+BC^2=(1/2)^2+1=5/4。
∴FC⊥平面ABCD,∴FC⊥CE,∴EF=√(FC^2+CE^2)=√[(1/2)^2+5/4]=√6/2。
容易求出:B1E=B1F=√[(1/2)^2+1]=√5/2。
∴sin[(1/2)∠EB1F]=(1/2)EF/B1E=(1/2)×(√6/2)/(√5/2)=√6/(2√5)。
∴cos∠EB1F=1-2{sin[(1/2)∠EB1F]}^2=1-2×6/(4×5)=2/5。
∵B1E∥MA、B1F∥NC,∴∠EB1F=AM与CN所成的角。
∴AM与CN所成角的余弦值是2/5。

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
