题目内容
已知l,m,n是三条不同的直线,α,β,γ是三个不同的平面,下列命题:
①若l∥m,n⊥m,则n⊥l;②若l∥m,m?α,则l∥α;③若l?α,m?β,α∥β,则l∥m; ④若α⊥γ,β⊥γ,α∩β=l,则l⊥γ.其中真命题是 .(写出所有真命题的序号).
①若l∥m,n⊥m,则n⊥l;②若l∥m,m?α,则l∥α;③若l?α,m?β,α∥β,则l∥m; ④若α⊥γ,β⊥γ,α∩β=l,则l⊥γ.其中真命题是
分析:根据异面直线所成角的定义可判断①是否正确;
根据线面平行的判定定理的条件判断②是否正确;
利用面面平行的性质知两平面内直线平行或异面;判断③是否正确;
借助图形,由面面垂直可得线面垂直,进而的线线垂直,再利用线面垂直的判定定理判断④是否正确.
根据线面平行的判定定理的条件判断②是否正确;
利用面面平行的性质知两平面内直线平行或异面;判断③是否正确;
借助图形,由面面垂直可得线面垂直,进而的线线垂直,再利用线面垂直的判定定理判断④是否正确.
解答:解:①中,由异面直线所成角的定义,直线l、m与n所成的角相等,∵n⊥m,∴n⊥l,故①正确;
②中,若l?α,也有l∥m,m?α,故②错误;
③中,若l?α,m?β,α∥β,则l与m的位置关系是平行或异面,故③错误;
④中,若α⊥γ,β⊥γ,α∩β=l,如图,
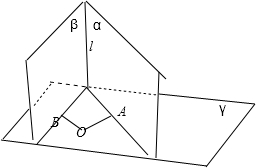
在平面γ内取点O,过O在γ内分别作OA,OB垂直于α与γ的交线和β与γ的交线,
则由面面垂直的性质得OA⊥α,OB⊥β,得:OA⊥l,OB⊥l,∴有l⊥γ,故④正确
故答案是①④.
②中,若l?α,也有l∥m,m?α,故②错误;
③中,若l?α,m?β,α∥β,则l与m的位置关系是平行或异面,故③错误;
④中,若α⊥γ,β⊥γ,α∩β=l,如图,

在平面γ内取点O,过O在γ内分别作OA,OB垂直于α与γ的交线和β与γ的交线,
则由面面垂直的性质得OA⊥α,OB⊥β,得:OA⊥l,OB⊥l,∴有l⊥γ,故④正确
故答案是①④.
点评:本题考查了面面垂直的判定与性质,考查了面面平行的判定及线线垂直的判定,考查了学生的空间想象能力,要牢记定理的条件.

练习册系列答案
相关题目

 是三个不同的平面,下列命题:
是三个不同的平面,下列命题: α,则l∥α;
α,则l∥α;