题目内容
已知l，m，n是三条不同的直线，α，β，γ是三个不同的平面，给出下列命题：
①若m∥l，m⊥α，则l⊥α；
②若m∥l，且m∥α，则l∥α；
③若α∩β=l，β∩γ=m，γ∩α=n，则l∥m∥n；
④若α∩γ=m，β∩γ=l，且α∥β，则m∥l．
其中真命题是（ ）
①若m∥l，m⊥α，则l⊥α；
②若m∥l，且m∥α，则l∥α；
③若α∩β=l，β∩γ=m，γ∩α=n，则l∥m∥n；
④若α∩γ=m，β∩γ=l，且α∥β，则m∥l．
其中真命题是（ ）
分析：根据平行线的性质结合直线与平面垂直的性质，得到①正确；根据平行线的性质和线面平行的判定，得到②错误；通过举实例说明，得到③错误；根据面面平行的性质定理及其证明过程，得到④正确．
解答：解：对于①，m⊥α说明直线m与平面α所成的角为90度，
因为m∥l，所以直线l与平面α所成的角等于直线m与平面α所成的角
所以l与平面α所成的角也为90度，l⊥α，故①正确；
对于②，若m∥l，且m∥α，可得l与α平行或l在α内，故②错误；
对于③，若α∩β=l，β∩γ=m，γ∩α=n，
以三棱柱为例，三个侧面分别为α、β、γ，它们的交线为三条侧棱，可得l∥m∥n，
再以三棱锥为例，三个侧面分别为α、β、γ，它们的交线为三条侧棱，可得l、m、n交于同一点，
所以l∥m∥n，或l、m、n交于同一点，故③错；
对于④，若α∥β，说明α、β没有公共点，再根据α∩γ=m，β∩γ=l，
说明m、l分别在α、β内，没有公共点，而且m、l共面于γ，
所以m∥l，故④正确．
综上所述，得①④为真命题，
故选C．
因为m∥l，所以直线l与平面α所成的角等于直线m与平面α所成的角
所以l与平面α所成的角也为90度，l⊥α，故①正确；
对于②，若m∥l，且m∥α，可得l与α平行或l在α内，故②错误；
对于③，若α∩β=l，β∩γ=m，γ∩α=n，
以三棱柱为例，三个侧面分别为α、β、γ，它们的交线为三条侧棱，可得l∥m∥n，
再以三棱锥为例，三个侧面分别为α、β、γ，它们的交线为三条侧棱，可得l、m、n交于同一点，
所以l∥m∥n，或l、m、n交于同一点，故③错；
对于④，若α∥β，说明α、β没有公共点，再根据α∩γ=m，β∩γ=l，
说明m、l分别在α、β内，没有公共点，而且m、l共面于γ，
所以m∥l，故④正确．
综上所述，得①④为真命题，
故选C．
点评：本题以命题真假的判断为载体，考查了空间的线面垂直、线面平行和面面平行的性质与判定等知识点，属于基础题．
练习册系列答案
相关题目
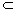
是三个不同的平面，下列命题：
α，则l∥α；