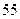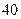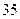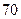题目内容
(本题满分14分)
已知数列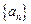 中,
中,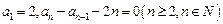 .
.
(1)写出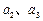 的值(只写结果)并求出数列
的值(只写结果)并求出数列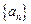 的通项公式;
的通项公式;
(2)设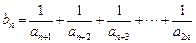 ,若对任意的正整数
,若对任意的正整数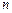 ,当
,当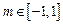 时,不等式
时,不等式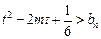 恒成立,求实数
恒成立,求实数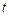 的取值范围。
的取值范围。
已知数列
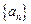 中,
中,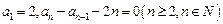 .
.(1)写出
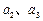 的值(只写结果)并求出数列
的值(只写结果)并求出数列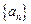 的通项公式;
的通项公式;(2)设
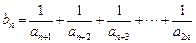 ,若对任意的正整数
,若对任意的正整数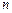 ,当
,当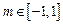 时,不等式
时,不等式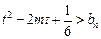 恒成立,求实数
恒成立,求实数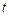 的取值范围。
的取值范围。(1)
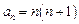
(2)
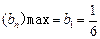
解:(1)∵
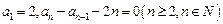 ∴
∴ 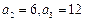 ……………2分
……………2分当
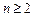 时,
时,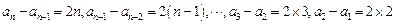 ,
,∴
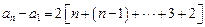 ,
,∴
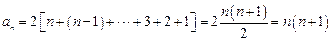 …………………5分
…………………5分当
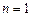 时,
时,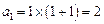 也满足上式, ∴数列
也满足上式, ∴数列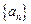 的通项公式为
的通项公式为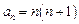 …6分
…6分(2)
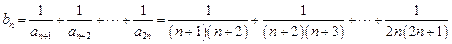
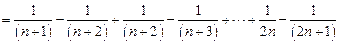
 …………………8分
…………………8分令
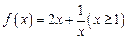 ,则
,则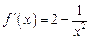 , 当
, 当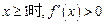 恒成立
恒成立∴
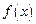 在
在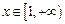 上是增函数,故当
上是增函数,故当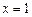 时,
时,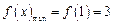
即当
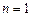 时,
时,  ……………11分
……………11分要使对任意的正整数
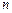 ,当
,当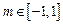 时,不等式
时,不等式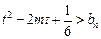 恒成立,
恒成立,则须使
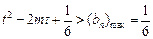 ,即
,即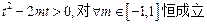 ,
,∴
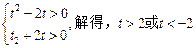
∴ 实数
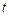 的取值范围为
的取值范围为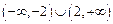 …14分
…14分另解:

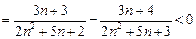
∴ 数列
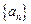 是单调递减数列,∴
是单调递减数列,∴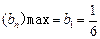

练习册系列答案
相关题目
 的前
的前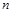 项和为
项和为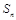 ,且
,且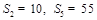 ,则过点
,则过点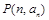 和
和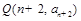
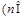 N*)的直线的一个方向向量的坐标可以是 ( )
N*)的直线的一个方向向量的坐标可以是 ( )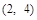
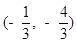
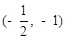
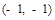
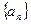 满足
满足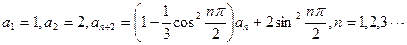
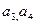 及数列
及数列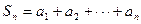 ,求
,求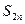 ;
;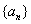 ,定义
,定义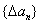 为数列
为数列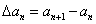 , (1)若数列
, (1)若数列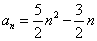 (
(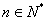 ),求:数列
),求:数列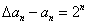 ,
, 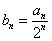 ,求证:数列
,求证:数列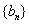 是等差数列,并求数列
是等差数列,并求数列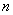 项和
项和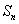
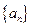 满足下列条件:
满足下列条件: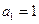 ,且对于任意的正整数
,且对于任意的正整数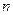 ,恒有
,恒有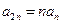 ,则
,则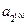 的值为 ( )
的值为 ( )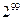
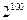
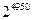
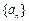 中,若
中,若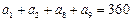 ,则数列
,则数列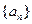 的前20项的和为100,那么
的前20项的和为100,那么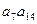 的最大值为 ( )
的最大值为 ( )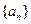 中,前
中,前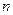 项和为
项和为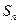 ,若
,若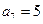 ,
,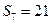 ,那么
,那么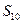 等于( )
等于( )