题目内容
数列 的前
的前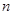 项和为
项和为 ,
,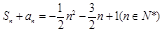 .
.
(Ⅰ)设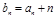 ,证明:数列
,证明:数列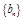 是等比数列;
是等比数列;
(Ⅱ)求数列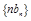 的前
的前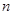 项和
项和 .
.
(Ⅲ)若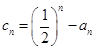 ,
,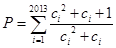 ,求不超过
,求不超过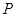 的最大的整数值.
的最大的整数值.
【答案】
(Ⅰ)详见解析;(Ⅱ)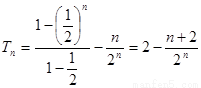 ;(Ⅲ)
;(Ⅲ)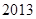 。
。
【解析】
试题分析:(Ⅰ)利用递推式相减后,构造等比数列进行证明;(Ⅱ)利用错位相减法求解;(Ⅲ)借助第一问的结论,确定数列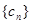 的通项公式,进而采用裂项相消法求解P,进而利用放缩求不超过
的通项公式,进而采用裂项相消法求解P,进而利用放缩求不超过 的最大的整数值.
的最大的整数值.
试题解析:(Ⅰ)因为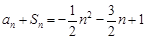 ,
,
所以 ①
当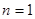 时,
时,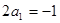 ,则
,则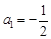 ,
1分
,
1分
② 当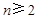 时,
时,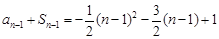 , 2分
, 2分
所以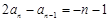 ,即
,即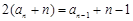 ,
,
所以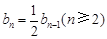 ,而
,而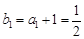 , 3分
, 3分
所以数列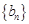 是首项为
是首项为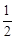 ,公比为
,公比为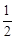 的等比数列,所以
的等比数列,所以 . 4分
. 4分
(Ⅱ)由(Ⅰ)得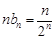 .
.
所以 ①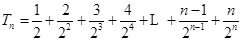 ,
,
②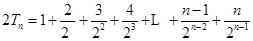 , 6分
, 6分
②-①得: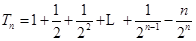 , 7分
, 7分
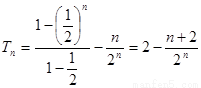 . 9分
. 9分
(Ⅲ)由(1)知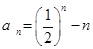
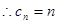 10分
10分
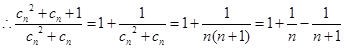 , 12分
, 12分
所以
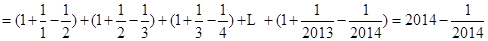 ,
,
故不超过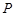 的最大整数为
的最大整数为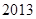 .
13分
.
13分
考点:1.等比数列的证明;2.数列求和。

练习册系列答案
相关题目
 为等差数列,
为等差数列, ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
 ,
, 的前
的前 ,求
,求 的大小,并说明理由.
的大小,并说明理由. 的前
的前 项和为
项和为 ,且对
,且对 都有
都有 ,则:
,则: ;
; 上述结果,归纳猜想数列
上述结果,归纳猜想数列 公式,并用数学归纳法加以证明.
公式,并用数学归纳法加以证明. .
. 的前
的前 项和为
项和为 ,且
,且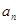 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: .
.