题目内容
数列 的前
的前 项和为
项和为 ,且
,且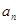 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
【答案】
(1)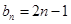 (2)略.
(2)略.
【解析】
试题分析:(1)应用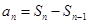 得到递推关系式,并判断为等比数列,写出
得到递推关系式,并判断为等比数列,写出 以及等差数列通项
以及等差数列通项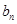 ;(2)应用裂项相消法求出
;(2)应用裂项相消法求出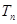 ,判断其单调性,得出证明.
,判断其单调性,得出证明.
试题解析:(1)∵ 是
是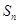 和
和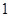 的等差中项,∴
的等差中项,∴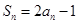 1分
1分
当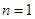 时,
时,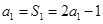 ,∴
,∴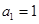 2分
2分
当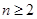 时,
时,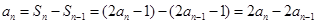 ,
,
∴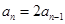 ,即
,即 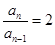 3分
3分
∴数列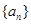 是以
是以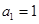 为首项,
为首项,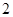 为公比的等比数列,
为公比的等比数列,
∴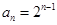 ,
,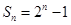 5分
5分
设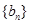 的公差为
的公差为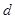 ,
,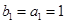 ,
,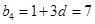 ,∴
,∴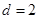 7分
7分
∴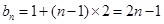 8分
8分
(2)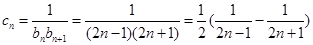 9分
9分
∴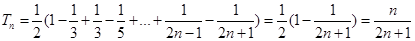 10分
10分
∵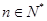 ,∴
,∴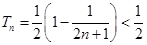 11分
11分
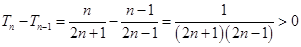
∴数列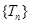 是一个递增数列
12分
是一个递增数列
12分
∴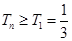 . 13分
. 13分
综上所述,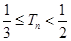 14分
14分
考点:等差数列等比数列的性质和应用,裂项相消法求数列前项和.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
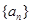 的前
的前 项和为
项和为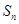 ,且
,且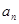 是
是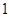 的等差中项,等差数列
的等差中项,等差数列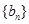 满足
满足 ,
, .
. ,数列
,数列 的前
的前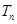 ,证明:
,证明: .
.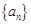 的前
的前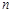 项和为
项和为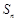 ,满足
,满足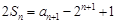 ,
,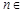
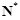 ,且
,且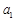 ,
,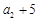 ,
,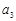 成等差数列.
成等差数列.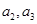 的值;
的值;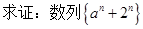 是等比数列
是等比数列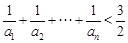 .
.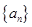 的前
的前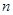 项和为
项和为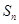 ,且
,且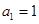 ,
,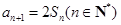 .则数列
.则数列