题目内容
(本小题14分)
数列 的前
的前 项和为
项和为 ,且对
,且对 都有
都有 ,则:
,则:
(1)求数列 的前三项
的前三项 ;
;
(2)根据 上述结果,归纳猜想数列
上述结果,归纳猜想数列 的通项
的通项 公式,并用数学归纳法加以证明.
公式,并用数学归纳法加以证明.
(3)求证:对任意 都有
都有 .
.
解:(1) …… 3分
…… 3分
(2)猜想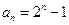 ,(
,( )…… 5
)…… 5 分
分
证明:①当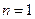 时,左边
时,左边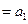 ,右边
,右边 ,猜测成立;…… 6分
,猜测成立;…… 6分
②假设当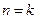 (
(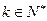 )时有
)时有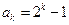 成立 …… 7分
成立 …… 7分
则当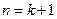 时,
时,
由 ,
,
 . …… 9分
. …… 9分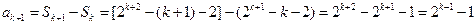
故猜测也成立. …… 10分
由①②可得对一切 ,数列
,数列 的通项公式为
的通项公式为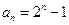 (
( )…… 11分
)…… 11分
(3) 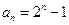 ,
, …… 12分
…… 12分
∴对任意 都有
都有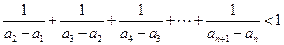 . …… 14分
. …… 14分
解析

练习册系列答案
相关题目
 列
列 中,
中, ,
,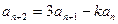 (k≠0)对任意
(k≠0)对任意 成立,令
成立,令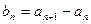 ,且
,且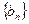 是等比数列.
是等比数列. (1)求实数
(1)求实数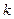 的值; (2)求数列
的值; (2)求数列
 的首项
的首项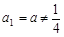 ,且
,且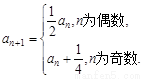
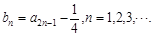
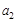 ,
, ;
; 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.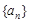 的通项公式.
的通项公式. 中,
中,  ,
, (k≠0)对任意
(k≠0)对任意 成立,令
成立,令 ,且
,且 是等比数列.
是等比数列. 的值; (2)求数列
的值; (2)求数列