题目内容
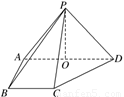
如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=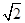 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角QACD的余弦值为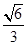 ?若存在,求出
?若存在,求出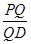 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)  (2)
(2)
 (3)存在,
(3)存在,
【解析】解:(1)在△PAD中,PA=PD,O为AD中点,所以PO⊥AD.又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD,所以PO⊥平面ABCD.
又在直角梯形ABCD中,连接OC,易得OC⊥AD,所以以O为坐标原点,OC,OD,OP所在直线分别为x,y,z轴建立空间直角坐标系,则P(0,0,1),A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),
∴ =(1,-1,-1),易证OA⊥平面POC,
=(1,-1,-1),易证OA⊥平面POC,
∴ =(0,-1,0)是平面POC的法向量,
=(0,-1,0)是平面POC的法向量,
cos〈 ,
, 〉=
〉= =
= .
.
∴直线PB与平面POC所成角的余弦值为 .
.
(2) =(0,1,-1),
=(0,1,-1), =(-1,0,1).
=(-1,0,1).
设平面PDC的一个法向量为u=(x,y,z),
则 取z=1,得u=(1,1,1).
取z=1,得u=(1,1,1).
∴B点到平面PCD的距离为
d= =
= .
.
(3)假设存在一点Q,则设 =λ
=λ (0<λ<1).
(0<λ<1).
∵. .=(0,1,-1),
.=(0,1,-1),
∴ =(0,λ,-λ)=
=(0,λ,-λ)= -
- ,
,
∴ =(0,λ,1-λ),∴Q(0,λ,1-λ).
=(0,λ,1-λ),∴Q(0,λ,1-λ).
设平面CAQ的一个法向量为m=(x,y,z),
又 =(1,1,0),AQ=(0,λ+1,1-λ),
=(1,1,0),AQ=(0,λ+1,1-λ),
则
取z=λ+1,得m=(1-λ,λ-1,λ+1),
又平面CAD的一个法向量为n=(0,0,1),
二面角QACD的余弦值为 ,
,
所以|cos〈m,n〉|= =
= ,
,
得3λ2-10λ+3=0,解得λ= 或λ=3(舍),
或λ=3(舍),
所以存在点Q,且 =
= .
.

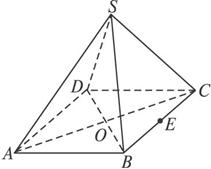
 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且P 为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且P 为AD的中点,Q为SB的中点.