题目内容
如图,在四棱锥S—ABCD中,侧棱SA=SB=SC=SD,底面ABCD是菱形,AC与BD交于O点.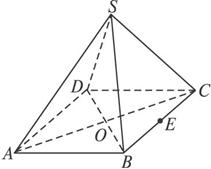
(1)求证:AC⊥平面SBD;
(2)若E为BC中点,点P在侧面△SCD内及其边界上运动,并保持PE⊥AC,试指出动点P的轨迹,并证明你的结论.
(1)证明:∵底面ABCD是菱形,O为中心,
∴AC⊥BD.
又SA=SC,
∴AC⊥SO.而SO∩BD=O,
∴AC⊥面SBD.
(2)解:取棱SC中点M,CD中点N,连结MN,
则动点P的轨迹即是线段MN.
证明:连结EM、EN,
∵E是BC中点,M是SC中点,
∴EM∥SB.同理,EN∥BD,∵AC⊥面SBD,∴AC⊥SB.
∴AC⊥EM.10分
同理,AC⊥EN,
又EM∩EN=E,
∴AC⊥面EMN.
因此,当P点在线段MN上运动时,总有AC⊥EP;
P点不在线段MN上时,不可能有AC⊥EP.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,