题目内容
已知关于x的一元二次函数f(x)=ax2-4bx+1
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4,},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在[1,+∞)上是增函数的概率;
(2)设点(a,b)是区域
内的随机点,求函数y=f(x)在[1,+∞)上是增函数的概率.
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4,},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在[1,+∞)上是增函数的概率;
(2)设点(a,b)是区域
|
分析:(1)分a=1,2,3,4,5 这五种情况来研究a>0,且
≤1的取法共有16种,而所有的取法共有6×6=36 种,从而求得所求事件的概率.
(2)由条件可得,实验的所有结果构成的区域Q 的面积等于S△OMN=
×8×8=32,满足条件的区域A的面积为
S△POM=
×8×
=
,故所求的事件的概率为 P=
,运算求得结果.
| 2b |
| a |
(2)由条件可得,实验的所有结果构成的区域Q 的面积等于S△OMN=
| 1 |
| 2 |
S△POM=
| 1 |
| 2 |
| 8 |
| 3 |
| 32 |
| 3 |
| S△POM |
| S△OMN |
解答:解:(1)由题意可得a>0,且
≤1,所有的取法共有6×6=36 种.
当a=1 时,b 只能取-2,-1这两个值.当a=2 时,b 只能取-2,-1,1 这三个值.
当a=3 时,b 只能取-2,-1,1 这三个值.当a=4 时,b 只能取-2,-1,1,2 这四个值.
当a=5 时,b 只能取-2,-1,1,2 这四个值.
故满足函数y=f(x)在[1,+∞)上是增函数的取法有 2+3+3+4+4=16种,
故所求事件的概率为
=
,故答案为:
.
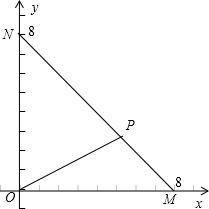
(2)由条件可得,实验的所有结果构成的区域为Q={(a,b)|
},如图所示,
该区域为一个三角形区域,其面积等于S△OMN=
×8×8=32.
满足函数y=f(x)在[1,+∞)上是增函数的基本事件构成的区域为A={(a,b)|
},
由
求得交点的坐标为P(
,
),故区域A的面积为 S△POM=
×8×
=
,
故所求的事件的概率为 P=
=
=
.
| 2b |
| a |
当a=1 时,b 只能取-2,-1这两个值.当a=2 时,b 只能取-2,-1,1 这三个值.
当a=3 时,b 只能取-2,-1,1 这三个值.当a=4 时,b 只能取-2,-1,1,2 这四个值.
当a=5 时,b 只能取-2,-1,1,2 这四个值.
故满足函数y=f(x)在[1,+∞)上是增函数的取法有 2+3+3+4+4=16种,
故所求事件的概率为
| 16 |
| 36 |
| 4 |
| 9 |
| 4 |
| 9 |
(2)由条件可得,实验的所有结果构成的区域为Q={(a,b)|
|
该区域为一个三角形区域,其面积等于S△OMN=
| 1 |
| 2 |
满足函数y=f(x)在[1,+∞)上是增函数的基本事件构成的区域为A={(a,b)|
|
由
|
| 16 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 32 |
| 3 |
故所求的事件的概率为 P=
| S△POM |
| S△OMN |
| ||
| 32 |
| 1 |
| 3 |

点评:本题考查等可能事件的概率,二次函数的单调区间以及简单的线性规划问题,画出实验的所有结果构成的区域Q
和区域A 的图形,是解题的关键.
和区域A 的图形,是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目