题目内容
（本小题满分12分）
定义在R上的函数f(x)满足：如果对任意x
,x
∈R，都有f(
)≤
［f(x
］，则称函数f(x)是R上的下凸函数.
已知二次函数f(x)= 
x
+x(∈R, ≠0).
（1）求证：当＞0时，函数f(x)是下凸函数.
（2）如果x∈［0,1］时，|f(x)|≤1都成立，试求实数的范围.
（1）对任意x
＞0,∴［f(x
)+ f (x
)］-2 f(
［
(
)］=x
≥0.
∴f(
≤
［f 
］. ∴函数f(x)是凹函数; （5分）
(2)由| f(x)|≤1
-1≤f(x) ≤1 -1≤
+x≤1.(*)
当x=0时，∈R;当x∈(0,1］时，(*)即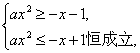
即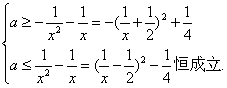
∵x∈(0,1］,∴
≥1.∴当=1时，-(+
)
-
取得最大值是-2；当=1时，(-)-取得最小值是0.
∴-2 ≤≤0 ,结合≠0，得-2≤＜0.综上，的范围是［-2,0).（12分）
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
