题目内容
对于x∈R,不等式|x-1|+|x-2|≥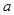 2+
2+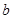 2恒成立,试求2
2恒成立,试求2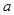 +
+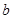 的最大值。
的最大值。
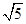
解析试题分析:本题主要考查恒成立问题、函数的最值、绝对值的运算性质、柯西不等式等基础知识,考查学生的转化能力、计算能力.先将“对于x∈R,不等式|x-1|+|x-2|≥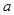 2+
2+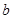 2恒成立”转化为“
2恒成立”转化为“ ”,利用绝对值的运算性质
”,利用绝对值的运算性质 求出最小值,得到
求出最小值,得到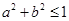 ,再利用柯西不等式
,再利用柯西不等式 求出
求出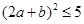 ,注意公式应用时等号成立的条件.
,注意公式应用时等号成立的条件.
试题解析:|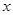 -1|+|
-1|+|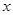 -2|=|
-2|=|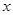 -1|+|2-
-1|+|2-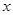 |≥|
|≥|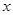 -1+2-
-1+2-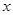 |="1" , 2分
|="1" , 2分
故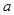 2+
2+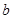 2≤1. 3分
2≤1. 3分
(2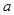 +
+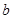 )2≤(22+12)(
)2≤(22+12)( 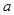 2+
2+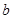 2) ≤5. 5分
2) ≤5. 5分
由
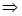
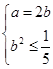 ,
,
即取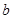 =
=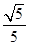 ,
,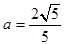 时等号成立.故(2
时等号成立.故(2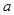 +
+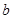 )max=
)max=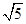 . 7分
. 7分
考点:恒成立问题、函数的最值、绝对值的运算性质、柯西不等式.

练习册系列答案
相关题目
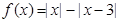
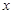 的不等式
的不等式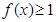 ;
;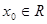 ,使得
,使得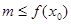 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
. ;
;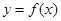 的最小值.
的最小值.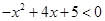 ;
;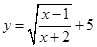 .
. .
. 的解集A;
的解集A;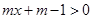 对任何
对任何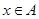 恒成立,求
恒成立,求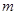 的取值范围.
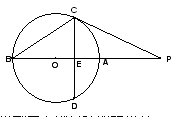
的取值范围.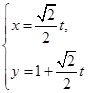 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为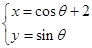 (
(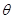 为参数),则圆心
为参数),则圆心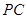 与圆
与圆 相切于点
相切于点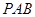 经过圆心
经过圆心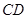 ⊥
⊥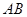 于点
于点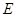 ,
,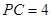 ,
,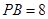 ,则
,则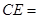 _________.
_________. 使
使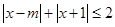 成立,则实数
成立,则实数
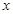 的不等式
的不等式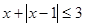 ;
;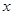 的不等式
的不等式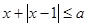 有解,求实数
有解,求实数 的取值范围.
的取值范围.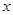 的不等式
的不等式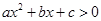 的解集为
的解集为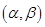 ,其中
,其中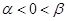 ,则关于
,则关于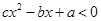 的解集为____________.
的解集为____________. 的不等式
的不等式 的解集为
的解集为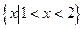 ,则实数
,则实数 的值为 .
的值为 .