题目内容
已知 的三内角
的三内角 、
、 、
、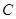 所对的边分别是
所对的边分别是 ,
,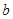 ,
,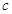 ,向量
,向量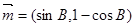 与向量
与向量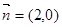 的夹角
的夹角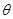 的余弦值为
的余弦值为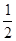
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若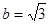 ,求
,求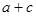 的范围。
的范围。
(Ⅰ)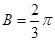 ;(Ⅱ)
;(Ⅱ)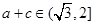 .
.
解析试题分析:(Ⅰ)向量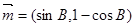 与向量
与向量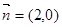 的夹角
的夹角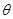 的余弦值为
的余弦值为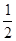 ,求角
,求角 的大小,由夹角公式,只需分别求出
的大小,由夹角公式,只需分别求出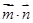 ,
,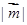 ,
, ,代入公式
,代入公式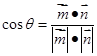 ,使
,使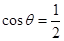 ,而
,而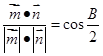 ,即
,即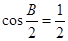 ,从而求出角
,从而求出角 的大小;(Ⅱ)若
的大小;(Ⅱ)若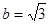 ,求
,求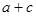 的范围,这是已知
的范围,这是已知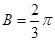 ,
,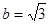 ,来求
,来求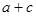 的范围,可考虑利用余弦定理来构造
的范围,可考虑利用余弦定理来构造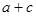 ,由余弦定理,得
,由余弦定理,得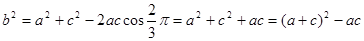 ,可考虑将
,可考虑将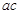 转化为
转化为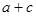 ,因此利用基本不等式进行转化
,因此利用基本不等式进行转化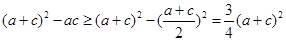 ,可得
,可得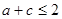 ,又有三角形两边之和大于第三边得
,又有三角形两边之和大于第三边得 ,从而求出
,从而求出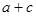 的范围.
的范围.
试题解析:(Ⅰ)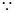
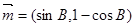 ,
,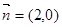 ,
, 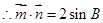 ,又
,又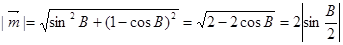 ,
,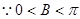 ,
, 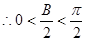 ,
, 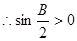 ,
,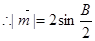 3分
3分
而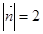 ,
, 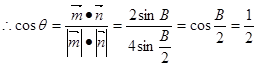 ,
, 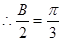 ,
, 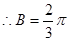 6分
6分
(Ⅱ)由余弦定理,得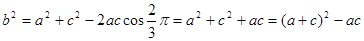
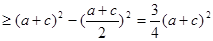 当且仅当
当且仅当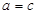 时,取等号,
时,取等号,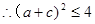
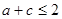 10分
10分
又
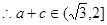 12分
12分
(其他解法请参照给分)
考点:向量的夹角,余弦定理,基本不等式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
设函数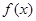 )定义为如下数表,且对任意自然数n均有xn+1=
)定义为如下数表,且对任意自然数n均有xn+1=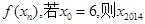 的值为( )
的值为( )
| A.1 | B.2 | C.4 | D.5 |
数列1,1,2,3,5,8,x,21,34,55中,x等于( )
| A.11 | B.12 | C.13 | D.14 |
 =
= +t
+t ,试问:
,试问: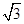 sin x,sin x),b="(cos" x,sin x),x∈
sin x,sin x),b="(cos" x,sin x),x∈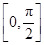 .
.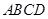 中,
中,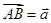 ,
,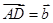 ,
,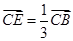 ,
,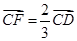 。
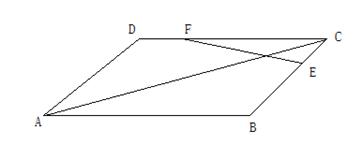
。
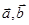 表示
表示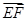 ;
;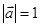 ,
,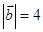 ,
,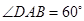 ,分别求
,分别求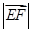 和
和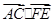 的值。
的值。 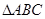 中,
中,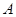 、
、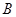 、
、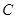 所对的边分别为
所对的边分别为 、
、 、
、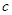 .已知向量
.已知向量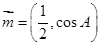 ,
,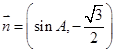 ,且
,且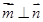 .
.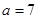 ,
,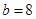 ,求
,求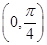 .
.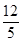 ,求sin
,求sin 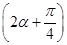 的值.
的值.