题目内容
在锐角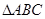 中,
中,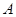 、
、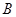 、
、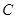 所对的边分别为
所对的边分别为 、
、 、
、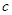 .已知向量
.已知向量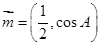 ,
,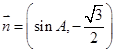 ,且
,且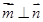 .
.
(1)求角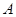 的大小;
的大小;
(2)若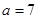 ,
,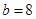 ,求
,求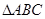 的面积.
的面积.
(1)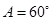 ;(2)
;(2)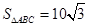 .
.
解析试题分析:(1)先根据平面向量垂直的等价条件得到等式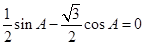 ,再利用弦化切的思想求出
,再利用弦化切的思想求出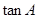 的值,最终在求出角
的值,最终在求出角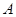 的值;(2)解法一:在角
的值;(2)解法一:在角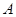 的大小确定的前提下,利用正弦定理与同角三角函数之间的关系求出
的大小确定的前提下,利用正弦定理与同角三角函数之间的关系求出 和
和 ,并利用
,并利用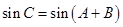 结合和角公式求出
结合和角公式求出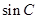 的值,最后利用面积公式
的值,最后利用面积公式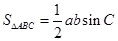 求出
求出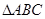 的面积;解法二:利用余弦定理求出
的面积;解法二:利用余弦定理求出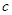 的值,并对
的值,并对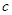 的值进行检验,然后面积公式
的值进行检验,然后面积公式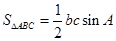 求出
求出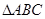 的面积.
的面积.
试题解析:(1)因为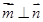 ,所以
,所以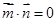 ,则
,则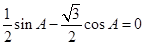 , 4分
, 4分
因为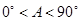 ,所以
,所以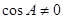 ,则
,则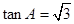 ,所以
,所以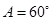 7分
7分
(2)解法一:由正弦定理得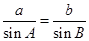 ,又
,又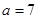 ,
,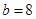 ,
,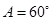 ,
,
则 ,因为
,因为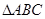 为锐角三角形,所以
为锐角三角形,所以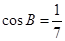 , 9分
, 9分
因为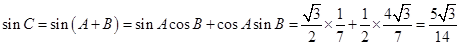 , 12分
, 12分
所以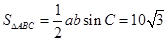 14分
14分
解法二:因为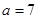 ,
,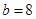 ,
,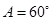 ,
,
所以由余弦定理可知,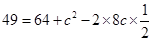 ,即
,即 ,解得
,解得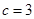 或
或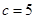 ,
,
当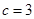 时,
时,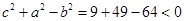 ,所以
,所以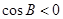 ,不合乎题意;
,不合乎题意;
当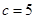 时,
时, ,所以
,所以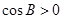 ,合乎题意;
,合乎题意;
所以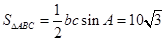 14分
14分
考点:正弦定理、余弦定理、同角三角函数的关系、两角和的正弦函数、三角形的面积公式

练习册系列答案
相关题目
已知数列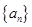 中,
中,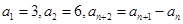 ,则
,则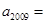 ( )
( )
| A.6 | B.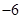 | C.3 | D.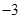 |
 个连续自然数按规律排成下表,根据规律,2011到2013,箭头的方向依次为( )
个连续自然数按规律排成下表,根据规律,2011到2013,箭头的方向依次为( )
| A.↓→ | B.→↑ | C.↑→ | D.→↓ |
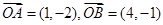 ,
,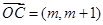 .
. 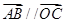 ,求实数
,求实数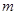 的值;
的值; 为直角三角形,求实数
为直角三角形,求实数 =λ
=λ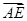 ,
,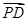 =μ
=μ ,
, =a,
=a, =b.
=b.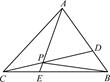
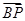 ;
; 的三内角
的三内角 、
、 、
、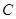 所对的边分别是
所对的边分别是 ,
,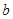 ,
,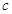 ,向量
,向量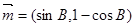 与向量
与向量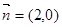 的夹角
的夹角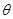 的余弦值为
的余弦值为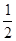
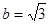 ,求
,求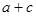 的范围。
的范围。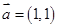 ,
,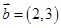 ,当
,当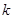 为何值时,
为何值时,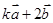 与
与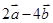 垂直?
垂直?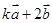 与
与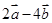 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?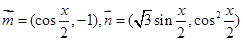 ,设函数
,设函数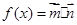
 在区间
在区间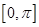 上的零点;
上的零点;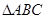 中,角
中,角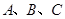 的对边分别是
的对边分别是 ,且满足
,且满足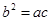 ,求
,求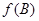 的取值范围.
的取值范围.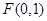 是中心在坐标原点
是中心在坐标原点 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆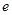 为
为 .
.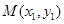 、
、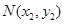 为椭圆
为椭圆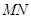 的斜率为
的斜率为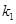 ;
; 是满足
是满足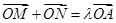 (
(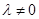 )的点,且直线
)的点,且直线 的斜率为
的斜率为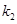 .
.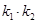 的值;
的值;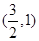 ,求实数
,求实数 的取值范围.
的取值范围.