题目内容
【题目】在 ![]() ,点M是△ABC外一点,BM=2CM=2,则AM的最大值与最小值的差为 .
,点M是△ABC外一点,BM=2CM=2,则AM的最大值与最小值的差为 .
【答案】2
【解析】解:取边BC的中点为O,则 ![]() =
= ![]() (
( ![]() ), 又
), 又 ![]() =0,∴
=0,∴ ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,∴△ABC为等腰三角形,
,∴△ABC为等腰三角形,
又∠A= ![]() ,∴△ABC为等边三角形,
,∴△ABC为等边三角形,
以O为坐标原点,以BC边所在的直线为x轴,
建立平面直角坐标系如图所示;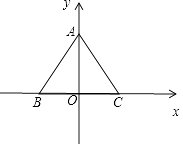
并设BC=2a( ![]() <a<
<a< ![]() ),点M(x,y);
),点M(x,y);
则A(0, ![]() a),B(﹣a,0),C(a,0),
a),B(﹣a,0),C(a,0),
又BM=CM=2,
所以(x+a)2+y2=4
(x﹣a)2+y2=1,
所以解方程组 ![]() 得:
得: 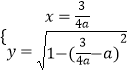 或
或 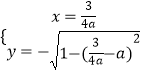 ,
,
所以当 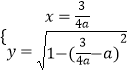 时
时 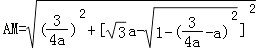
= ![]()
= ![]()
= ![]() ,
,
令a2﹣ ![]() =cosθ,
=cosθ,
则AM= ![]() =
= ![]() ,
,
所以当θ= ![]() 时(AM)min=1,
时(AM)min=1,
同理当 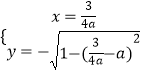 时,
时,
AM= ![]() =
= ![]() =
= ![]() ,
,
所以当θ= ![]() 时(AM)max=3;
时(AM)max=3;
综上可知:AM的取值范围是[1,3],
AM的最大值与最小值的差是2.
所以答案是:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目