题目内容
已知函数g(x)=
mx2-2x+l+ln(x+l)(m≥1).
(1)若曲线C:y=g(x)在点P(0,1)处的切线l与曲线C有且只有一个公共点,求m的值;
(2)求证:函数g(x)存在单凋减区间[a,b];
(3)若c=b-a,求c的取值范围.
| 1 | 2 |
(1)若曲线C:y=g(x)在点P(0,1)处的切线l与曲线C有且只有一个公共点,求m的值;
(2)求证:函数g(x)存在单凋减区间[a,b];
(3)若c=b-a,求c的取值范围.
分析:(1)利用导数的几何意义求出切线的斜率,进而求出切线的方程,由切线l与曲线C有且只有一个公共点,转化为二者的方程联立的方程组有且只有一个解0,再利用导数即可得出;
(2)函数g(x)存在单凋减区间[a,b]?g′(x)<0,再由m≥1,x>-1,利用二次函数的性质即可证明;
(3)利用(2)的结论及一元二次方程的根与系数的关系及不等式的性质即可求出.
(2)函数g(x)存在单凋减区间[a,b]?g′(x)<0,再由m≥1,x>-1,利用二次函数的性质即可证明;
(3)利用(2)的结论及一元二次方程的根与系数的关系及不等式的性质即可求出.
解答:解:(1)∵函数g(x)=
mx2-2x+1+ln(x+1)(m≥1),定义域为(-1,+∞).
∴g′(x)=mx-2+
,∴g′(0)=-2+1=-1.
∴切线l的方程为:y-1=-x,即y=-x+1,
∵切线l与曲线C有且只有一个公共点,
∴
mx2-2x+1+ln(x+1)=-x+1有且只有一个解0.
令h(x)=
mx2-x+ln(x+1),
则h′(x)=mx-1+
=
,
①当m=1时,h′(x)=
≥0,h(x)在(-1,+∞)上单调递增,满足有且只有一个解0.
②当m>1时,(
-1)∈(-1,0),令h′(x)=0,解得x=0或
-1.
列表如下:
由表格画出图象: 当x→-1时,h(x)→-∞,h(
当x→-1时,h(x)→-∞,h(
-1)>h(0)=0,故在区间(-1,
-1)内还有一个交点,
即方程h(x)=0由两个实数根,与已知有且仅有一个解矛盾,应舍去.
综上可知:只有m=1满足题意.
(2)由g′(x)=mx-2+
=
<0(x>-1)?mx2+(m-2)x-1<0.
令f(x)=mx2+(m-2)x-1(x>-1,m≥1).
则△=(m-2)2+4m=m2+4>0,且其对称轴x=-
=
-
>-1,
f(-1)=1>0,
∴函数f(x)在(-1,+∞)上必有两个不等实数根a=
,b=
.
使得函数g(x)在区间[a,b]上单调递减.
(3)由(2)可知:a+b=
,ab=-
,
∴c=b-a=
=
=
,
∵m≥1,∴1<
≤
.
∴c的取值范围是(1,
].
| 1 |
| 2 |
∴g′(x)=mx-2+
| 1 |
| x+1 |
∴切线l的方程为:y-1=-x,即y=-x+1,
∵切线l与曲线C有且只有一个公共点,
∴
| 1 |
| 2 |

令h(x)=
| 1 |
| 2 |
则h′(x)=mx-1+
| 1 |
| x+1 |
mx[x-(
| ||
| x+1 |
①当m=1时,h′(x)=
| mx2 |
| x+1 |
②当m>1时,(
| 1 |
| m |
| 1 |
| m |
列表如下:
由表格画出图象:
 当x→-1时,h(x)→-∞,h(
当x→-1时,h(x)→-∞,h(| 1 |
| m |
| 1 |
| m |
即方程h(x)=0由两个实数根,与已知有且仅有一个解矛盾,应舍去.
综上可知:只有m=1满足题意.
(2)由g′(x)=mx-2+
| 1 |
| x+1 |
| mx2+(m-2)x-1 |
| x+1 |
令f(x)=mx2+(m-2)x-1(x>-1,m≥1).
则△=(m-2)2+4m=m2+4>0,且其对称轴x=-
| m-2 |
| 2m |
| 1 |
| m |
| 1 |
| 2 |
f(-1)=1>0,
∴函数f(x)在(-1,+∞)上必有两个不等实数根a=
(2-m)-
| ||
| 2m |
(2-m)+
| ||
| 2m |
使得函数g(x)在区间[a,b]上单调递减.
(3)由(2)可知:a+b=
| 2-m |
| m |
| 1 |
| m |
∴c=b-a=
| (b-a)2 |
| (b+a)2-4ab |
1+
|
∵m≥1,∴1<
1+
|
| 5 |
∴c的取值范围是(1,
| 5 |
点评:熟练掌握利用导数研究函数的性质及“三个二次”的关系是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
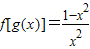 ,则f(0)= .
,则f(0)= .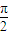 x+2ψ)(0<ψ<
x+2ψ)(0<ψ< )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )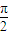 x+2ψ)(0<ψ<
x+2ψ)(0<ψ< )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )