题目内容
已知函数g(x)=1-2x,f[g(x)]=
,则f(0)=
| 1-x2 | x2 |
3
3
.分析:可以令g(x)=0求出x的值,然后代入f[g(x)]的表达式求解,亦可以采用换元法求出f(x)的表达式再求解.
解答:解:法一:令g(x)=0即1-2x=0,得x=
,
将x=
代入
得f[g(x)]=3.
法二:f[g(x)]=f(1-2x)=
,
令1-2x=t得x=
,代入上式有:
f(t)=
,
令t=0得:f(0)=3.
故答案为3.
| 1 |
| 2 |
将x=
| 1 |
| 2 |
| 1-x2 |
| x2 |
法二:f[g(x)]=f(1-2x)=
| 1-x2 |
| x2 |
令1-2x=t得x=
| 1-t |
| 2 |
f(t)=
| 3+2t-t2 |
| 1-2t+t2 |
令t=0得:f(0)=3.
故答案为3.
点评:本题采用了两种解法,其中换元法是求解析式常用的方法,有时要注意换元后变量的取值范围.

练习册系列答案
相关题目
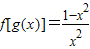 ,则f(0)= .
,则f(0)= .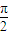 x+2ψ)(0<ψ<
x+2ψ)(0<ψ< )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )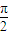 x+2ψ)(0<ψ<
x+2ψ)(0<ψ< )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )