题目内容
(1)确定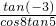 的符号;
的符号;
(2)已知α∈(0,π),且sinα+cosα=m(0<m<1),试判断式子sinα-cosα的符号.
解:(1)∵-3,5,8分别是第三、第四、第二象限角,
∴tan(-3)>0,tan5<0,cos8<0,
∴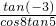 >0.
>0.
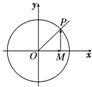 (2)若0<α<
(2)若0<α< ,则如图所示,在单位圆中,OM=cosα,MP=sinα,
,则如图所示,在单位圆中,OM=cosα,MP=sinα,
∴sinα+cosα=MP+OM>OP=1.
若α= ,则sinα+cosα=1.
,则sinα+cosα=1.
由已知0<m<1,故α∈( ,π).
,π).
于是有sinα-cosα>0.
分析:(1)根据1弧度对应的角大小,判断出-3,5,8所在的象限,再判断出对应三角函数的符号,即得出式子的符号;
(2)根据三角函数线和α∈(0,π)且sinα+cosα=m(0<m<1),判断出α的具体范围,再得出式子sinα-cosα的符号.
点评:本题的考点是三角函数的符号应用,即先判断出角的象限,再根据“一全正二正弦三正切四余弦”来判断,对于比较复杂的可借助于三角函数线判断.
∴tan(-3)>0,tan5<0,cos8<0,
∴
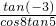 >0.
>0. (2)若0<α<
(2)若0<α< ,则如图所示,在单位圆中,OM=cosα,MP=sinα,
,则如图所示,在单位圆中,OM=cosα,MP=sinα,∴sinα+cosα=MP+OM>OP=1.
若α=
 ,则sinα+cosα=1.
,则sinα+cosα=1.由已知0<m<1,故α∈(
 ,π).
,π).于是有sinα-cosα>0.
分析:(1)根据1弧度对应的角大小,判断出-3,5,8所在的象限,再判断出对应三角函数的符号,即得出式子的符号;
(2)根据三角函数线和α∈(0,π)且sinα+cosα=m(0<m<1),判断出α的具体范围,再得出式子sinα-cosα的符号.
点评:本题的考点是三角函数的符号应用,即先判断出角的象限,再根据“一全正二正弦三正切四余弦”来判断,对于比较复杂的可借助于三角函数线判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
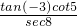 的符号;
的符号;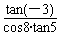 的符号;
的符号;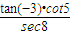 的符号;
的符号;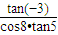 的符号;
的符号;