Question

(本小题满分12分)

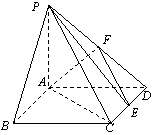
如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA＝AD，点F是棱PD的中点，点E在棱CD上移动.

⑴ 当点E为CD的中点时，试判断直线EF

与平面PAC的关系，并说明理由；

⑵ 求证：PE⊥AF.

Answer 1

解：(Ⅰ)当点为CD的中点时，平面PAC.      ……………2分

       理由如下：

点分别为，的中点，_.        …………3分

，_，平面PAC.       ………4分

(Ⅱ)， , _.

又是矩形，_,，_.

 , _.…………6分

，点是的中点,  _.  …………8分

又_{,    .}  ………………10分

    .     ………………12分