题目内容
对于非零实数a,b,以下四个命题都成立:
①a+![]() ≠0;②(a+b)2=a2+2ab+b2;③若|a|=|b|,则a=±b;④若a2=ab,则a=b.那么,对于非零复数a,b,仍然成立的命题的所有序号是________.
≠0;②(a+b)2=a2+2ab+b2;③若|a|=|b|,则a=±b;④若a2=ab,则a=b.那么,对于非零复数a,b,仍然成立的命题的所有序号是________.
解析:取a=i,则a+![]() =i+
=i+![]() =0,可得命题①对非零复数不成立;
=0,可得命题①对非零复数不成立;
命题②(a+b)2=a2+2ab+b2为所有数均成立的恒等式,故命题②对非零复数也成立;
取a=1,b=i,可得|a|=|b|,但a≠±b,∴命题③对非零复数不成立;
若a2=ab,则a(a-b)=0,由于a,b为非零复数,∴a-b=0,即a=b,∴命题④对非零复数也成立.
综上可得对非零复数a,b,仍然成立的命题的所有序号是②④.
答案:②④

练习册系列答案
相关题目
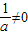 ;②(a+b)2=a2+2ab+b2;③若a2=ab,则a=b
;②(a+b)2=a2+2ab+b2;③若a2=ab,则a=b 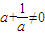 ;②(a+b)2=a2+2ab+b2;
;②(a+b)2=a2+2ab+b2;