题目内容
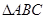 的内角
的内角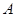 、
、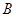 、
、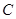 的对边分别为
的对边分别为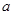 、
、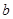 、
、 ,已知
,已知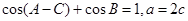 ,求
,求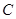 。
。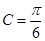 。
。试题分析:由
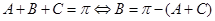 ,
,由正弦定理及
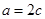 可得
可得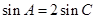
所以
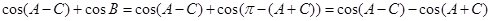
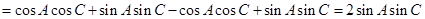
故由
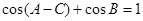 与
与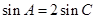 可得
可得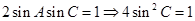
而
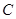 为三角形的内角且
为三角形的内角且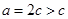 ,故
,故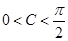 ,所以
,所以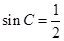 ,故
,故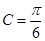 。
。点评:中档题,综合考查了正弦定理的应用、诱导公式、两角和与差的三角函数公式,能较好地考查学生的计算能力及转化与化归思想,求角时要特别注意三角形内角的范围。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
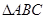 的内角
的内角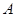 、
、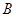 、
、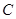 的对边分别为
的对边分别为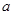 、
、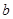 、
、 ,已知
,已知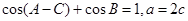 ,求
,求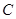 。
。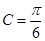 。
。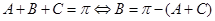 ,
,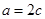 可得
可得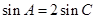
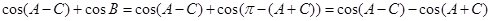
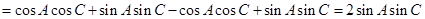
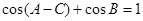 与
与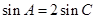 可得
可得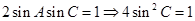
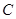 为三角形的内角且
为三角形的内角且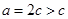 ,故
,故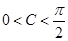 ,所以
,所以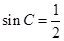 ,故
,故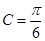 。
。
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案